Regresión lineal desde cero con NumPy

Regresión lineal con NumPy

 

Motivación

 

La Regresión Lineal es una de las herramientas más fundamentales en el aprendizaje automático. Se utiliza para encontrar una línea recta que se ajuste bien a nuestros datos. Aunque solo funciona con patrones simples de líneas rectas, entender las matemáticas detrás de ella nos ayuda a comprender los métodos de Descenso de Gradiente y Minimización de Pérdida. Estos son importantes para modelos más complicados utilizados en todas las tareas de aprendizaje automático y aprendizaje profundo.

• Las 5 Mejores Herramientas de IA para Maximizar la Productividad
• Utilizando OCR para dibujos de ingeniería complejos
• Desvelando el futuro de la IA con GPT-4 y la IA Explicada (XAI)

En este artículo, nos pondremos manos a la obra y construiremos la Regresión Lineal desde cero utilizando NumPy. En lugar de utilizar implementaciones abstractas como las proporcionadas por Scikit-Learn, comenzaremos desde lo básico.

 

Conjunto de datos

 

Generamos un conjunto de datos ficticio utilizando métodos de Scikit-Learn. Por ahora, solo utilizamos una variable, pero la implementación será general y podrá entrenarse con cualquier número de características.

El método make_regression proporcionado por Scikit-Learn genera conjuntos de datos de regresión lineal aleatorios, con ruido gaussiano añadido para agregar algo de aleatoriedad.

X, y = datasets.make_regression(
        n_samples=500, n_features=1, noise=15, random_state=4)

 

Generamos 500 valores aleatorios, cada uno con una única característica. Por lo tanto, X tiene forma (500, 1) y cada uno de los 500 valores independientes de X tiene un valor y correspondiente. Así que, y también tiene forma (500, ).

Visualmente, el conjunto de datos se ve así:

   

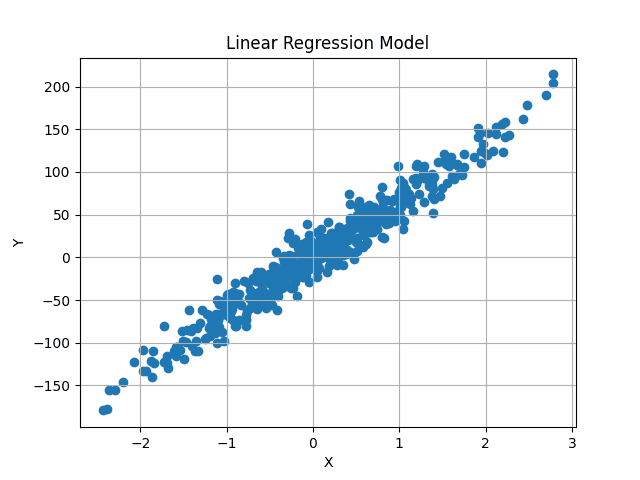
Nuestro objetivo es encontrar una línea de mejor ajuste que pase por el centro de estos datos, minimizando la diferencia promedio entre los valores de y predichos y los valores de y originales.

 

Intuición

 

La ecuación general para una línea lineal es:

y = m*X + b

X es numérico, de un solo valor. Aquí, m y b representan la pendiente e intersección en y (o sesgo). Estos son desconocidos, y valores variables de estos pueden generar diferentes líneas. En el aprendizaje automático, X depende de los datos, al igual que los valores de y. Solo tenemos control sobre m y b, que actúan como nuestros parámetros del modelo. Nuestro objetivo es encontrar valores óptimos para estos dos parámetros, que generen una línea que minimice la diferencia entre los valores de y predichos y los valores de y reales.

Esto se extiende al escenario en el que X es multidimensional. En ese caso, el número de valores m será igual al número de dimensiones en nuestros datos. Por ejemplo, si nuestros datos tienen tres características diferentes, tendremos tres valores m diferentes, llamados pesos.

La ecuación ahora se convierte en:

y = w1*X1 + w2*X2 + w3*X3 + b

Esto puede extenderse a cualquier número de características.

Pero, ¿cómo sabemos los valores óptimos de nuestro sesgo y pesos? Bueno, no lo sabemos. Pero podemos encontrarlos de forma iterativa utilizando el Descenso de Gradiente. Comenzamos con valores aleatorios y los modificamos ligeramente durante varias etapas hasta que nos acerquemos a los valores óptimos.

Primero, inicialicemos la Regresión Lineal, y luego repasaremos el proceso de optimización con más detalle.

 

Inicializar la Clase de Regresión Lineal

 

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

 

Utilizamos una tasa de aprendizaje y un número de iteraciones como hiperparámetros, que se explicarán más adelante. Los pesos y sesgos se establecen como None porque el número de parámetros de peso depende de las características de entrada dentro de los datos. Aún no tenemos acceso a los datos, por lo que los inicializamos como None por ahora.

 

El método Fit

 

En el método fit, se nos proporcionan los datos y sus valores asociados. Ahora podemos utilizar estos para inicializar nuestros pesos y luego entrenar el modelo para encontrar los pesos óptimos.

def ajustar(self, X, y):
        num_muestras, num_caracteristicas = X.shape     # forma de X [N, f]
        self.pesos = np.random.rand(num_caracteristicas)  # forma de W [f, 1]
        self.bias = 0

 

La característica independiente X será una matriz NumPy de forma (num_muestras, num_caracteristicas). En nuestro caso, la forma de X es (500, 1). Cada fila en nuestros datos tendrá un valor objetivo asociado, por lo que y también tiene forma (500,) o (num_muestras).

Extraemos esto e inicializamos aleatoriamente los pesos dados el número de características de entrada. Ahora nuestros pesos también son una matriz NumPy de tamaño (num_caracteristicas, ). El sesgo es un solo valor inicializado en cero.

 

Prediciendo Valores de Y

 

Usamos la ecuación de la recta discutida anteriormente para calcular los valores de y predichos. Sin embargo, en lugar de un enfoque iterativo para sumar todos los valores, podemos seguir un enfoque vectorizado para una computación más rápida. Dado que los pesos y los valores de X son matrices NumPy, podemos usar la multiplicación de matrices para obtener predicciones.

X tiene forma (num_muestras, num_caracteristicas) y los pesos tienen forma (num_caracteristicas, ). Queremos que las predicciones tengan forma (num_muestras, ) para que coincidan con los valores originales de y. Por lo tanto, podemos multiplicar X por los pesos, o (num_muestras, num_caracteristicas) x (num_caracteristicas, ) para obtener predicciones de forma (num_muestras, ).

El valor del sesgo se agrega al final de cada predicción. Esto se puede implementar fácilmente en una sola línea.

# La forma de y_pred debe ser N, 1
y_pred = np.dot(X, self.pesos) + self.bias

 

¿Sin embargo, estas predicciones son correctas? Obviamente no. Estamos usando valores inicializados aleatoriamente para los pesos y el sesgo, por lo que las predicciones también serán aleatorias.

¿Cómo obtenemos los valores óptimos? Descenso del Gradiente.

 

Función de Pérdida y Descenso del Gradiente

 

Ahora que tenemos tanto los valores de y predichos como los objetivos, podemos encontrar la diferencia entre ambos valores. El Error Cuadrático Medio (MSE) se utiliza para comparar números de valor real. La ecuación es la siguiente:

   

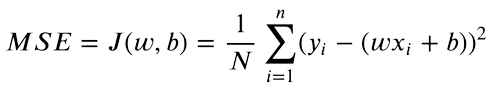
Solo nos importa la diferencia absoluta entre nuestros valores. Una predicción mayor que el valor original es tan mala como una predicción menor. Por lo tanto, elevamos al cuadrado la diferencia entre nuestro valor objetivo y las predicciones, para convertir las diferencias negativas en positivas. Además, esto penaliza una diferencia más grande entre los objetivos y las predicciones, ya que las diferencias más altas al cuadrado contribuirán más a la pérdida final.

Para que nuestras predicciones estén lo más cerca posible de los objetivos originales, ahora intentamos minimizar esta función. La función de pérdida será mínima cuando el gradiente sea cero. Como solo podemos optimizar nuestros valores de pesos y sesgo, tomamos las derivadas parciales de la función MSE con respecto a los valores de pesos y sesgo.

   

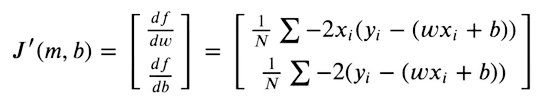
Luego optimizamos nuestros pesos dados los valores del gradiente, utilizando el Descenso del Gradiente.

   

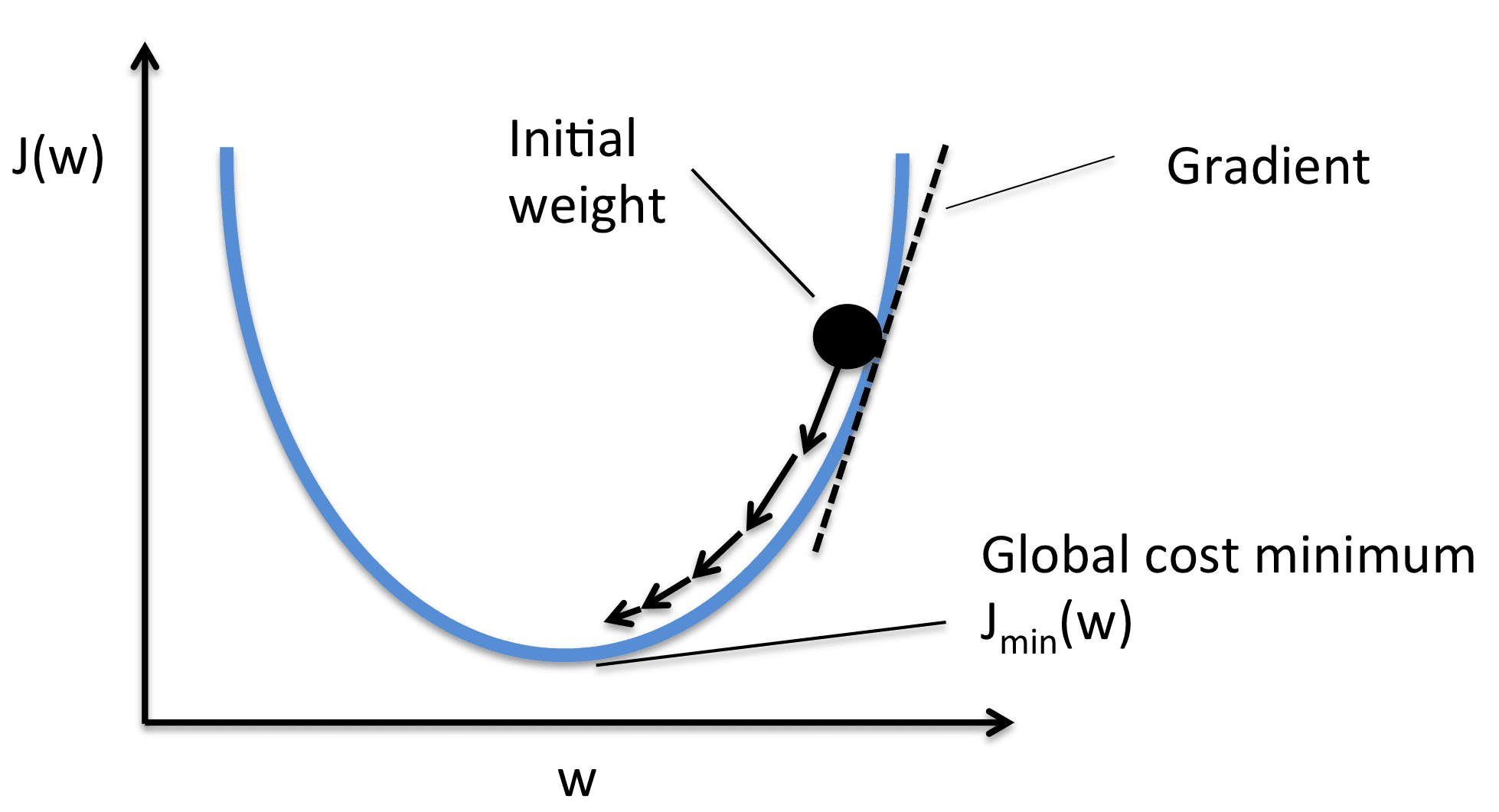
Tomamos el gradiente con respecto a cada valor de peso y luego los movemos al opuesto del gradiente. Esto empuja la pérdida hacia el mínimo. Según la imagen, el gradiente es positivo, por lo que disminuimos el peso. Esto empuja el J(W) o la pérdida hacia el valor mínimo. Por lo tanto, las ecuaciones de optimización son las siguientes:

   

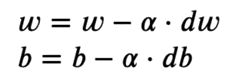
La tasa de aprendizaje (o alfa) controla los pasos incrementales que se muestran en la imagen. Solo hacemos un cambio pequeño en el valor, para un movimiento estable hacia el mínimo.

 

Implementación

 

Si simplificamos la ecuación de derivada usando manipulación algebraica básica, esto se vuelve muy simple de implementar.

   

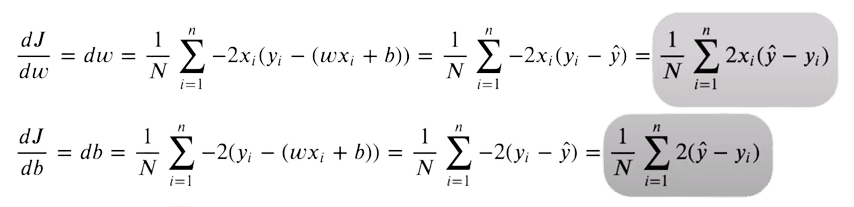
Para la derivada, implementamos esto usando dos líneas de código:

# X -> [ N, f ]
# y_pred -> [ N ]
# dw -> [ f ]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)

 

dw tiene nuevamente una forma de (num_features, ) por lo que tenemos un valor de derivada separado para cada peso. Los optimizamos por separado. db tiene un solo valor.

Para optimizar los valores ahora, movemos los valores en la dirección opuesta del gradiente usando una resta básica.

self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db

 

Nuevamente, esto es solo un paso. Solo hacemos un pequeño cambio a los valores inicializados aleatoriamente. Ahora realizamos repetidamente los mismos pasos para converger hacia un mínimo.

El bucle completo es el siguiente:

for i in range(self.n_iters):

            # y_pred debe tener forma N, 1
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

 

Predicción

 

Predicimos de la misma manera que lo hicimos durante el entrenamiento. Sin embargo, ahora tenemos el conjunto óptimo de pesos y sesgos. Los valores predichos ahora deberían estar cerca de los valores originales.

def predict(self, X):
        return np.dot(X, self.weights) + self.bias

 

Resultados

 

Con pesos y sesgos inicializados aleatoriamente, nuestras predicciones fueron las siguientes:

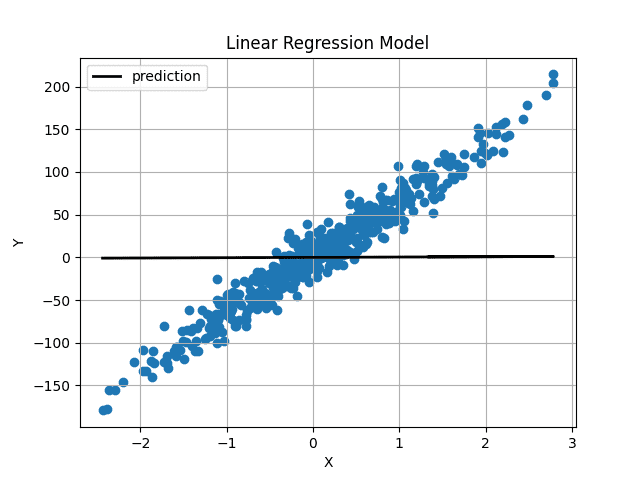  Imagen de Autor   Los pesos y sesgos se inicializaron muy cerca de 0, por lo que obtenemos una línea horizontal. Después de entrenar el modelo durante 1000 iteraciones, obtenemos esto:

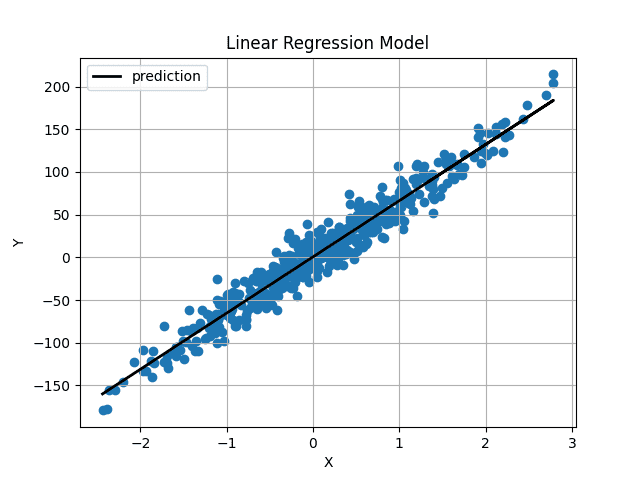  Imagen de Autor  

La línea predicha pasa justo por el centro de nuestros datos y parece ser la línea de mejor ajuste posible. 

 

Conclusión

 

Ahora has implementado Regresión Lineal desde cero. El código completo también está disponible en GitHub.

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        num_samples, num_features = X.shape     # X forma [N, f]
        self.weights = np.random.rand(num_features)  # W forma [f, 1]
        self.bias = 0

        for i in range(self.n_iters):

            # y_pred debe tener forma N, 1
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

        return self

    def predict(self, X):
        return np.dot(X, self.weights) + self.bias

    Muhammad Arham es un Ingeniero de Aprendizaje Profundo que trabaja en Visión por Computadora y Procesamiento del Lenguaje Natural. Ha trabajado en la implementación y optimización de varias aplicaciones de IA generativa que alcanzaron los primeros lugares en Vyro.AI. Está interesado en construir y optimizar modelos de aprendizaje automático para sistemas inteligentes y cree en la mejora continua.  

We will continue to update Zepes; if you have any questions or suggestions, please contact us!