El Problema de Enrutamiento de Vehículos Soluciones Exactas y Heurísticas

Problema de Enrutamiento de Vehículos Soluciones Exactas y Heurísticas

Comprender cómo resolver problemas de enrutamiento complejos con Python

El Problema de Enrutamiento de Vehículos (VRP, por sus siglas en inglés) tiene como objetivo determinar el mejor conjunto de rutas que deben ser realizadas por una flota de vehículos para atender a un conjunto dado de clientes. Debido a sus diversas aplicaciones y desafiantes aspectos combinatorios, es uno de los problemas más estudiados en Investigación de Operaciones y Optimización Numérica.

El Problema de Enrutamiento de Vehículos Capacitado (CVRP, por sus siglas en inglés) es una de las variantes más comunes, ya que introduce vehículos con capacidad de carga limitada y posiblemente restricciones de duración/distancia. Otras variantes habituales también introducen múltiples depósitos, flotas heterogéneas, recogidas y entregas, y restricciones de ventanas de tiempo.

Los aspectos combinatorios de estos problemas son tales que al considerar un simple conjunto de 15 puntos, existen 6 × 10¹¹ rutas posibles que los conectan (Dantzig & Ramser, 1959). Por lo tanto, algunas aplicaciones del mundo real seguirían siendo impracticables hasta que la investigación computacional y algorítmica avanzara en las últimas décadas. Los algoritmos de Ramificación, Corte y Precio han logrado demostrar la optimalidad de las instancias de CVRP con unos pocos cientos de clientes (Fukasawa et al., 2006; Pecin et al., 2017), y las metaheurísticas de última generación combinadas con técnicas de búsqueda local pueden proporcionar soluciones de buena calidad (a veces óptimas) para estas instancias en unos pocos segundos (Vidal et al., 2012; Vidal, 2022).

A lo largo de este artículo, presentaremos el Problema de Enrutamiento de Vehículos Capacitado con restricciones de carga (y duración) y lo resolveremos utilizando Programación Entera Mixta (MIP, por sus siglas en inglés) y algoritmos (meta)heurísticos especializados. En la primera parte, utilizaremos Python AML Pyomo, con el solucionador HiGHS, mientras que en la segunda parte utilizaremos el paquete Google OR Tools.

• ¿Qué es la Inteligencia de Negocios?
• Por qué deberías preocuparte por la Ley de IA de la UE hoy
• Generative AI para Audio y Música de AudioCraft Meta

El lector que esté más interesado en aplicaciones del mundo real que en aspectos teóricos del problema puede revisar rápidamente la sección de MIP y prestar más atención a las secciones de (Meta)Heurísticas Especializadas y Extensiones Útiles.

Aquellos interesados en comprender en detalle la formulación de MIP pero que aún no están familiarizados con la optimización numérica pueden encontrar útil echar un vistazo a mis historias anteriores sobre Programación Lineal y el método de Ramificación y Acotación antes de continuar con esta.

Como de costumbre, puedes encontrar el código completo en este repositorio de git.

¡Ahora, sumerjámonos!

Programación Entera Mixta

La formulación matemática presentada en esta sección utilizará las mismas ecuaciones presentadas por Toth & Vigo (2002) en el modelo al que se hace referencia como la “formulación de flujo de vehículos de tres índices”.

Consideremos un conjunto V de nodos (demandas y depósito) y un conjunto K de vehículos. Utilizaremos minúsculas i y j para indicar los índices de los nodos y minúscula k para indicar los índices de los vehículos. Como este modelo es válido para el caso asimétrico, supongamos que los nodos son parte de un grafo dirigido completo G(V, A) con arcos A. En este problema, hay un solo nodo de depósito indexado por 0 y todos los vehículos tienen la misma capacidad Q. Consideremos dos grupos de variables de decisión:

• x_{i, j, k}: Es una variable binaria que indica un arco activo desde el nodo i al nodo j realizado por el vehículo k.
• y_{i, k}: Es una variable binaria que indica que la demanda del nodo i es satisfecha por el vehículo k.

Consideremos nuestro objetivo de minimizar el valor del costo asociado con los arcos activos. La duración total o la distancia son ejemplos habituales. Supongamos que el costo de atravesar el arco i, j es cᵢⱼ. La función objetivo se puede expresar de la siguiente manera.

También debemos incluir restricciones que aseguren:

• Cada cliente i es visitado una vez, por lo tanto tiene un arco activo que parte de él y uno que llega a él.
• Si alguna variable de arco indexada por el vehículo k entra en un nodo i o sale de él, la demanda q de este nodo se asigna al vehículo k.
• La demanda total asignada a un vehículo no debe exceder su capacidad Q.
• Exactamente |K| nodos comienzan en el depósito y llegan al depósito.
• No hay subtours… Sin embargo, el número de subtours es potencialmente demasiado grande para ser enumerado desde el principio. Nos adentraremos en más detalles sobre cómo hacerlo.

Como es habitual en los tutoriales de Python, comencemos la parte práctica importando las bibliotecas utilizadas en esta sección:

import time
from itertools import cycle
import numpy as np
from scipy.spatial.distance import pdist, squareform
import matplotlib.pyplot as plt
import matplotlib as mpl
import networkx as nx
import pyomo.environ as pyo
from pyomo.contrib.appsi.solvers.highs import Highs

Y ahora instanciemos un problema aleatorio con N nodos de demanda. En este ejemplo, se asume que el nodo del depósito es el primer nodo (índice 0), por lo que nos aseguramos de que su demanda correspondiente también sea cero.

np.random.seed(42)  # Los resultados deben ser siempre los mismos
N = 10
demands = np.random.randint(1, 10, size=N)
demands[0] = 0
capacity = 15
n_vehicles = 4
coordinates = np.random.rand(N, 2)
distances = squareform(pdist(coordinates, metric="euclidean"))
distances = np.round(distances, decimals=4)  # evitar errores numéricos

El número de vehículos necesarios se puede calcular utilizando un Problema de Empaquetamiento de Contenedores. También se incluye un ejemplo de cómo realizarlo en el código fuente completo.

Hay dos enfoques para modelar un problema en pyomo: modelos abstractos y concretos. En el primer enfoque, se definen las expresiones algebraicas del problema antes de suministrar algunos valores de datos, mientras que, en el segundo, se crea la instancia del modelo inmediatamente a medida que se definen sus elementos. Puede encontrar más información sobre estos enfoques en la documentación de la biblioteca o en el libro de Bynum et al. (2021). A lo largo de este artículo, adoptaremos la formulación del modelo concreto.

model = pyo.ConcreteModel()

Instanciemos ahora los conjuntos de nodos de demanda V, arcos A y vehículos K. Observe que el nodo del depósito se incluye en el conjunto de nodos V como en la formulación matemática original.

model.V = pyo.Set(initialize=range(len(demands)))
model.A = pyo.Set(initialize=[(i, j) for i in model.V for j in model.V if i != j])
model.K = pyo.Set(initialize=range(n_vehicles))

Ahora nuestros parámetros para capacidad, carga de demanda y costos de arco.

model.Q = pyo.Param(initialize=capacity)
model.q = pyo.Param(model.V, initialize={i: d for (i, d) in enumerate(demands)})
model.c = pyo.Param(model.A, initialize={(i, j): distances[i, j] for (i, j) in model.A})

También debemos incluir las restricciones previamente enumeradas. Primero, implementémoslas utilizando la firma habitual de Pyomo: función(modelo, *dominio).

def arcs_in(modelo, i):
    if i == modelo.V.first():
        return sum(modelo.x[:, i, :]) == len(modelo.K)
    else:
        return sum(modelo.x[:, i, :]) == 1.0

def arcs_out(modelo, i):
    if i == modelo.V.first():
        return sum(modelo.x[i, :, :]) == len(modelo.K)
    else:
        return sum(modelo.x[i, :, :]) == 1.0

def vehicle_assignment(modelo, i, k):
    return sum(modelo.x[:, i, k]) == modelo.y[i, k]

def comp_vehicle_assignment(modelo, i, k):
    return sum(modelo.x[i, :, k]) == modelo.y[i, k]

def capacity_constraint(modelo, k):
    return sum(modelo.y[i, k] * modelo.q[i] for i in modelo.V) <= modelo.Q

Y luego incorporemos estas restricciones en nuestro modelo.

model.arcs_in = pyo.Constraint(model.V, rule=arcs_in)
model.arcs_out = pyo.Constraint(model.V, rule=arcs_out)
model.vehicle_assignment = pyo.Constraint(model.V, model.K, rule=vehicle_assignment)
model.comp_vehicle_assignment = pyo.Constraint(model.V, model.K, rule=comp_vehicle_assignment)
model.capacity_constraint = pyo.Constraint(model.K, rule=capacity_constraint)

Observe que aún no incluí las restricciones de eliminación de subtours. Deberíamos considerar todas las permutaciones posibles de los N nodos tomando k a la vez y estas podrían ser prohibitivamente grandes para enumerar incluso para instancias de tamaño moderado. Alternativamente, en nuestro procedimiento de solución, incluiremos recursivamente restricciones de eliminación de subtours cada vez que se encuentre una nueva solución si verificamos que esta solución produce subtours. En algunos solvers comerciales, se llaman “restricciones perezosas” y se pueden incorporar directamente en el solver a través de una devolución de llamada.

Primero creemos una función que, dada una subruta, todos los nodos restantes, un nodo de la subruta y un vehículo, devuelva una expresión de Pyomo correspondiente a la formulación matemática previamente establecida. Además, incluyamos una ConstraintList a la que agregaremos nuevos elementos a medida que avanzamos con la solución.

def eliminacion_subruta(modelo, S, Sout, h, k):    nodos_fuera = sum(modelo.x[i, j, k] for i in S for j in Sout)    return modelo.y[h, k] <= nodos_fuera modelo.eliminacion_subruta = pyo.ConstraintList()

Debemos crear algunas funciones que, dada una solución, devuelvan las subrutas creadas (si existen). Para hacerlo, primero crearemos una lista de arcos activos en el modelo utilizando la función find_arcs. Esta lista se utilizará para crear un grafo dirigido incompleto utilizando la clase DiGraph de Networkx. Y la función find_subtours debería devolver una lista de conjuntos de componentes conectados.

def find_arcs(modelo):    arcos = []    for i, j in modelo.A:        for k in modelo.K:            if np.isclose(modelo.x[i, j, k].value, 1):                arcos.append((i, j))    return arcosdef find_subtours(arcos):    G = nx.DiGraph(arcos)    subrutas = list(nx.strongly_connected_components(G))    return subrutas

Nuestro objetivo es eliminar grupos de componentes conectados que no incluyan el nodo del depósito. Por lo tanto, en el siguiente paso, crearemos funciones que iteren sobre la lista de conjuntos e incluyan nuevas restricciones si el conjunto de componentes no incluye el nodo del depósito. Esto utilizará el método add de la clase ConstraintList.

def eliminar_subrutas(modelo, subrutas):    proceder = False    for S in subrutas:        if 0 not in S:            proceder = True            Sout = {i for i in modelo.V if i not in S}            for h in S:                for k in modelo.K:                    modelo.eliminacion_subruta.add(                      eliminacion_subruta(modelo, S, Sout, h, k)                    )    return proceder

Y ahora tenemos todo listo para proponer un procedimiento de solución que resuelva iterativamente el MIP, verifique si la solución actual tiene subrutas y, si es así, incluya nuevas restricciones para eliminarlas. De lo contrario, la solución encontrada es óptima.

def resolver_paso(modelo, solucionador):    sol = solucionador.solve(modelo)    arcos = find_arcs(modelo)    subrutas = find_subtours(arcos)    time.sleep(0.1)    proceder = eliminar_subrutas(modelo, subrutas)    return sol, proceder def resolver(modelo, solucionador):    proceder = True    while proceder:        sol, proceder = resolver_paso(modelo, solucionador)    return sol

Ahora instanciemos el solucionador y resolvamos nuestro modelo. El solucionador Highs está disponible en Pyomo (verifica las importaciones) si el paquete highspy está instalado. Así que asegúrate de ejecutar un pip install highspy.

solucionador = Highs()solucionador.highs_options = {    "log_file": "Highs.log",    "mip_heuristic_effort": 0.2,    "mip_detect_symmetry": True,    "mip_rel_gap": 1e-6,}solucion = resolver(modelo, solucionador)

Una función más para encontrar las rutas creadas y estamos listos para mostrar los resultados.

def encontrar_rutas(modelo):    rutas = []    for k in modelo.K:        nodo = 0        rutas.append([0])        while True:            for j in modelo.V:                if (nodo, j) in modelo.A:                    if np.isclose(modelo.x[nodo, j, k].value, 1):                        nodo = j                        rutas[-1].append(nodo)                        break            if nodo == 0:                break    return rutas

Resultados increíbles para la pequeña instancia con un total de 10 nodos. Sin embargo, incluso para esta pequeña instancia, el solucionador tardó casi medio minuto en obtener la solución y la complejidad aumenta significativamente con más puntos de demanda. Afortunadamente, hay algoritmos especializados disponibles públicamente para encontrar soluciones de buena calidad para instancias mucho más grandes en poco tiempo computacional. Veamos esto en la siguiente sección.

Metaheurísticas Especializadas

A lo largo de los años se han propuesto varias metaheurísticas especializadas para variantes del VRP. La mayoría de ellas se basan fuertemente en algoritmos de búsqueda local, de modo que, dada una solución, se prueban diferentes perturbaciones para mejorar secuencialmente su costo hasta que no sea posible mejorar más en el vecindario dado. Cuando se utiliza Google Or Tools, también utilizaremos métodos de búsqueda local asociados con algoritmos constructivos.

En esta sección, se utilizará la instancia 150d de Rochat y Taillard (1995). Sus datos se obtuvieron de CVRPLIB. Esta instancia tiene 150 clientes y un nodo de depósito, por lo que seguramente no podríamos resolverlo utilizando la estrategia MIP presentada anteriormente.

Comencemos una vez más importando las bibliotecas utilizadas.

from itertools import cycleimport numpy as npimport pandas as pdfrom scipy.spatial.distance import pdist, squareformimport matplotlib.pyplot as pltimport matplotlib as mplfrom ortools.constraint_solver import routing_enums_pb2from ortools.constraint_solver import pywrapcp

Y carguemos los datos del problema desde un archivo que incluye las coordenadas y la demanda de cada nodo.

dataset = pd.read_csv("./data/tai150d.csv", index_col=0)coordinates = dataset.loc[:, ["x", "y"]]demands = dataset.d.valuescapacity = 1874n_vehicles = 15N = coordinates.shape[0]distances = squareform(pdist(coordinates, metric="euclidean"))distances = np.round(distances, decimals=4)

El primer paso para utilizar el solucionador de VRP de OR Tools es instanciar un administrador de enrutamiento y un modelo.

# Crear el administrador de índice de enrutamiento: número de nodos, número de vehículos, nodo de depósitomanager = pywrapcp.RoutingIndexManager(    N, n_vehicles, 0)# Crear el modelo de enrutamientorouting = pywrapcp.RoutingModel(manager)

A continuación, incluiremos devoluciones de llamada para cuantificar dimensiones relacionadas con arcos/bordes y nodos. El método RegisterTransitCallback de nuestra instancia de enrutamiento se puede utilizar para cuantificar cualquier dimensión relacionada con arcos/bordes, mientras que el método RegisterUnaryTransitCallback puede cuantificar valores relacionados con nodos.

# Mismo válido para cualquier devolución de llamada relacionada con arcos/bordesdef distance_callback(from_index, to_index):    from_node = manager.IndexToNode(from_index)    to_node = manager.IndexToNode(to_index)    return distances[from_node, to_node]transit_callback_index = routing.RegisterTransitCallback(distance_callback)# Mismo válido para cualquier devolución de llamada relacionada con nodosdef demand_callback(from_index):    from_node = manager.IndexToNode(from_index)    return demands[from_node]demand_callback_index = routing.RegisterUnaryTransitCallback(demand_callback)

Ahora, incluiremos una restricción de capacidad utilizando el demand_callback_index definido previamente. Observa que las restricciones de duración podrían haberse definido utilizando la misma sintaxis simplemente pasando instancias de RegisterTransitCallback como primer argumento. Además, es importante destacar que el modelo de enrutamiento maneja flotas heterogéneas, por lo que debemos pasar una lista de valores en el tercer argumento.

# Cualquier restricción asociada con los vehículos puede tomar los mismos argumentosrouting.AddDimensionWithVehicleCapacity(    demand_callback_index,    0,  # holgura de capacidad nula    [capacity,] * n_vehicles,  # capacidades máximas de vehículos (lista para cada vehículo)    True,  # inicio de acumulación a cero    'Capacidad')

De manera similar, la definición del objetivo también toma una devolución de llamada como argumento principal. En este ejemplo, minimicemos las distancias definidas en transit_callback_index.

routing.SetArcCostEvaluatorOfAllVehicles(transit_callback_index)

Por último, debemos definir los parámetros del solucionador y resolver nuestro modelo.

# Configurando estrategias heurísticassearch_parameters = pywrapcp.DefaultRoutingSearchParameters()search_parameters.first_solution_strategy = (    routing_enums_pb2.FirstSolutionStrategy.CHRISTOFIDES)search_parameters.local_search_metaheuristic = (    routing_enums_pb2.LocalSearchMetaheuristic.GUIDED_LOCAL_SEARCH)search_parameters.time_limit.FromSeconds(300)# Resolver el problemasolution = routing.SolveWithParameters(search_parameters)

El siguiente fragmento de código se puede utilizar para extraer las rutas utilizadas en nuestra solución.

tours = []for vehicle_id in range(n_vehicles):    index = routing.Start(vehicle_id)    tours.append([])    while not routing.IsEnd(index):        node_index = manager.IndexToNode(index)        previous_index = index        index = solution.Value(routing.NextVar(index))        tours[-1].append(node_index)    else:        node_index = manager.IndexToNode(index)        tours[-1].append(node_index)

Y se puede acceder al valor objetivo ejecutando la línea simple solution.ObjectiveValue(). Usando la configuración presentada, obtuve un objetivo de 2679, que está bastante cerca del valor óptimo probado de 2645 (1.2% de diferencia). Las rutas obtenidas se representan a continuación.

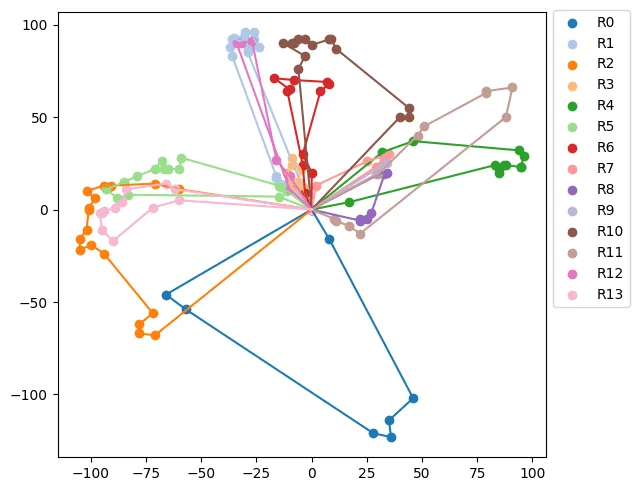
El código completo (incluyendo los gráficos) está disponible en este repositorio git.

Extensiones Útiles

La biblioteca de OR Tools es fantástica como un solucionador general para problemas de enrutamiento, ya que maneja varias variantes del VRP, como ventanas de tiempo, flotas heterogéneas y múltiples depósitos. Sin embargo, los algoritmos adecuados para el CVRP canónico pueden funcionar aún mejor. Vale la pena echarle un vistazo al paquete HGS-CVRP (Vidal, 2022) que combina un algoritmo genético de última generación con varios movimientos de búsqueda local. El algoritmo encuentra la solución óptima para la instancia tai150d en menos de 20 segundos.

En cuanto a algunas aplicaciones del mundo real, es probable que uno deba basarse en distancias (o duraciones) por carretera en lugar de distancias euclidianas para conectar ubicaciones. Google proporciona una interfaz de pago agradable para hacerlo, que puedes consultar en este tutorial. Sin embargo, si estás buscando alternativas de código abierto, vale la pena consultar la API de OpenStreetMap. Algunas solicitudes útiles son:

• https://router.project-osrm.org/table/v1/driving/<UBICACIONES>
• http://router.project-osrm.org/route/v1/car/<UBICACIONES>?overview=false&steps=true

En donde <UBICACIONES> debe ser una lista de pares de longitud y latitud separados por comas dentro de los pares y por puntos y comas entre diferentes pares. También puedes especificar fuentes y destinos en la solicitud de tabla, lo cual es útil en caso de que la tabla completa sea demasiado grande para manejarla en una sola solicitud.

Además de realizar cálculos de enrutamiento precisos, la visualización puede ser una herramienta importante. La biblioteca de Python folium puede ser bastante útil para hacerlo. Definitivamente vale la pena echarle un vistazo.

Lectura Adicional

Anteriormente en este artículo implementamos un modelo MIP exacto para el CVRP, que no es adecuado para instancias de tamaño moderado. Sin embargo, los algoritmos que combinan la generación de columnas con el Branch and Cut han tenido éxito en la resolución de instancias con hasta unos pocos cientos de clientes. Vale la pena echarle un vistazo a los documentos de investigación de Fukasawa et al. (2006) y Pecin et al. (2017).

Aquellos interesados en una introducción previa a la generación de columnas pueden encontrarla en mi artículo anterior de VoAGI.

En cuanto a las metaheurísticas, los documentos de Vidal et al. (2012) y Vidal (2022) son fantásticos. Ambos también están disponibles en forma de informes técnicos, con enlaces disponibles en el repositorio de HGS-CVRP.

Conclusiones

En este artículo se presentaron dos enfoques para resolver el Problema de Enrutamiento de Vehículos con Capacidad (CVRP): Programación Entera Mixta y (Meta)Heurísticas. La primera alternativa se utilizó para resolver una pequeña instancia en la que ha tenido éxito, aunque no puede manejar instancias de tamaño moderado o grande. El segundo enfoque se utilizó para resolver un problema desafiante de la literatura con 150 clientes, para el cual el solucionador encontró una solución de buena calidad con una diferencia del 1.2% respecto al óptimo conocido en 300s.

Referencias

Bynum, M. L. et al., 2021. Pyomo-optimization modeling in python. Springer.

Dantzig, G. B., & Ramser, J. H., 1959. The truck dispatching problem. Management science, 6(1), 80–91.

Fukasawa, R., Longo, H., Lysgaard, J., Aragão, M. P. D., Reis, M., Uchoa, E., & Werneck, R. F., 2006. Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Mathematical programming, 106, 491–511.

Pecin, D., Pessoa, A., Poggi, M., & Uchoa, E., 2017. Mejora de la técnica branch-cut-and-price para enrutamiento de vehículos con capacidad. Mathematical Programming Computation, 9, 61–100.

Rochat, Y., & Taillard, É. D., 1995. Diversificación y intensificación probabilísticas en la búsqueda local para el enrutamiento de vehículos. Journal of heuristics, 1, 147–167.

Toth, P., & Vigo, D., 2002. Una visión general de los problemas de enrutamiento de vehículos. The vehicle routing problem, 1–26.

Vidal, T., 2022. Búsqueda genética híbrida para el CVRP: implementación de código abierto y vecindario SWAP*. Computers & Operations Research, 140, 105643.

Vidal, T., Crainic, T. G., Gendreau, M., Lahrichi, N., & Rei, W., 2012. Un algoritmo genético híbrido para problemas de enrutamiento de vehículos multidepósito y periódicos. Operations Research, 60(3), 611–624.

We will continue to update Zepes; if you have any questions or suggestions, please contact us!