Optimización del controlador PID Un enfoque de descenso de gradiente

Optimización del controlador PID mediante descenso de gradiente

Utilizando el aprendizaje automático para resolver problemas de optimización de ingeniería

Aprendizaje automático. Aprendizaje profundo. IA. Cada día más personas utilizan estas tecnologías. Esto se ha visto impulsado en gran medida por el surgimiento de los Modelos de Lenguaje Grande implementados por ChatGPT, Bard y otros. A pesar de su amplio uso, relativamente pocas personas están familiarizadas con los métodos subyacentes de estas tecnologías.

En este artículo, nos adentramos en uno de los métodos fundamentales utilizados en el aprendizaje automático: el algoritmo de descenso de gradiente.

En lugar de ver el descenso de gradiente a través del prisma de las redes neuronales, donde se utiliza para optimizar los pesos y sesgos de la red, examinaremos el algoritmo como una herramienta para resolver problemas clásicos de optimización de ingeniería.

En concreto, utilizaremos el descenso de gradiente para ajustar las ganancias de un controlador PID (Proporcional-Integral-Derivativo) para un sistema de control de velocidad de crucero de un automóvil.

• LLM (Modelos de Lenguaje Grandes) para un Mejor Aprendizaje del Desarrollador de tu Producto
• Conoce a WebAgent el nuevo LLM de DeepMind que sigue instrucciones y completa tareas en sitios web
• El modelo POE de sistemas de hardware inspirados en la biología

La motivación para seguir este enfoque es doble:

En primer lugar, optimizar los pesos y sesgos en una red neuronal es un problema de alta dimensión. Hay muchas partes en movimiento y creo que estas distraen de la utilidad subyacente del descenso de gradiente para resolver problemas de optimización.

En segundo lugar, como verán, el descenso de gradiente puede ser una herramienta poderosa cuando se aplica a problemas clásicos de ingeniería como la sintonización de controladores PID, la cinemática inversa en robótica y la optimización de topología. El descenso de gradiente es una herramienta que, en mi opinión, más ingenieros deberían conocer y poder utilizar.

Después de leer este artículo, comprenderá qué es un controlador PID, cómo funciona el algoritmo de descenso de gradiente y cómo se puede aplicar para resolver problemas clásicos de optimización de ingeniería. Es posible que se sienta motivado para utilizar el descenso de gradiente para abordar desafíos de optimización propios.

Todo el código utilizado en este artículo está disponible aquí en GitHub.

¿Qué es un controlador PID?

Un controlador PID es un mecanismo de control de retroalimentación ampliamente utilizado en ingeniería y sistemas automatizados. Su objetivo es mantener un punto de consigna deseado ajustando continuamente la señal de control en función del error entre el punto de consigna y la salida medida del sistema (la variable de proceso).

Los controladores PID tienen aplicaciones extensas en diversas industrias y ámbitos. Se utilizan ampliamente en sistemas de control de procesos, como el control de temperatura en la fabricación, el control de flujo en plantas químicas y el control de presión en sistemas de HVAC. Los controladores PID también se utilizan en robótica para posicionamiento preciso y control de movimiento, así como en sistemas automotrices para el control del acelerador, la regulación de la velocidad del motor y los sistemas antibloqueo de frenos. Juegan un papel vital en aplicaciones aeroespaciales y de aviación, incluidos los pilotos automáticos de aeronaves y los sistemas de control de actitud.

Un controlador PID consta de tres componentes: el término proporcional, el término integral y el término derivativo. El término proporcional proporciona una respuesta inmediata al error actual, el término integral acumula y corrige los errores pasados, y el término derivativo predice y contrarresta las tendencias de error futuras.

El lazo de control de un controlador PID se presenta en el diagrama de bloques anterior. r(t) es el punto de consigna y y(t) es la variable de proceso. La variable de proceso se resta del punto de consigna para obtener la señal de error, e(t).

La señal de control, u(t), es la suma de los términos proporcional, integral y derivativo. La señal de control se ingresa al proceso y esto, a su vez, hace que la variable de proceso se actualice.

Señal de control del controlador PID u(t)

El algoritmo de descenso de gradiente

El descenso de gradiente es un algoritmo de optimización comúnmente utilizado en el aprendizaje automático y la optimización matemática. Su objetivo es encontrar el mínimo de una función de costo dada ajustando iterativamente los parámetros en función del gradiente de la función de costo. El gradiente apunta en la dirección del ascenso más pronunciado, por lo que tomando pasos en la dirección opuesta, el algoritmo converge gradualmente hacia la solución óptima.

Un solo paso de actualización de descenso de gradiente se define como:

Paso de actualización de descenso de gradiente

Donde aₙ es un vector de parámetros de entrada. El subíndice n denota la iteración. f(aₙ) es una función de coste multivariable y ∇f(a) es el gradiente de esa función de coste. ∇f(aₙ) representa la dirección de ascenso más pronunciado, por lo que se resta de aₙ para reducir la función de coste en la siguiente iteración. 𝛾 es la tasa de aprendizaje que determina el tamaño del paso en cada iteración.

Se debe seleccionar un valor apropiado para 𝛾. Si es demasiado grande, los pasos tomados en cada iteración serán demasiado grandes y harán que el algoritmo de descenso de gradiente no converja. Si es demasiado pequeño, el algoritmo de descenso de gradiente será computacionalmente costoso y llevará mucho tiempo converger.

El descenso de gradiente se aplica en una amplia gama de campos y disciplinas. En el aprendizaje automático y el aprendizaje profundo, es un algoritmo de optimización fundamental utilizado para entrenar redes neuronales y optimizar sus parámetros. Mediante la actualización iterativa de los pesos y sesgos de la red en función del gradiente de la función de coste, el descenso de gradiente permite que la red aprenda y mejore su rendimiento con el tiempo.

Más allá del aprendizaje automático, el descenso de gradiente se utiliza en diversos problemas de optimización en ingeniería, física, economía y otros campos. Ayuda en la estimación de parámetros, la identificación de sistemas, el procesamiento de señales, la reconstrucción de imágenes y muchas otras tareas que requieren encontrar el mínimo o máximo de una función. La versatilidad y eficacia del descenso de gradiente lo convierten en una herramienta esencial para resolver problemas de optimización y mejorar modelos y sistemas en diversos campos.

Optimización de los coeficientes de un controlador PID mediante descenso de gradiente

Existen varios métodos disponibles para ajustar un controlador PID. Estos incluyen el método de ajuste manual y métodos heurísticos como el método de Ziegler-Nichols. El método de ajuste manual puede ser lento y puede requerir múltiples iteraciones para encontrar valores óptimos, mientras que el método de Ziegler-Nichols a menudo produce coeficientes agresivos y gran sobreimpulso, lo que significa que no es adecuado para ciertas aplicaciones.

Se presenta aquí un enfoque de descenso de gradiente para la optimización de un controlador PID. Optimizaremos el sistema de control de un control de crucero de un automóvil sujeto a un cambio repentino en el punto de consigna.

Controlando la posición del pedal, el objetivo del controlador es acelerar el automóvil hasta la velocidad deseada con un mínimo sobreimpulso, tiempo de asentamiento y error en estado estable.

El automóvil está sujeto a una fuerza de conducción proporcional a la posición del pedal. Las fuerzas de resistencia al rodaje y resistencia aerodinámica actúan en dirección opuesta a la fuerza de conducción. La posición del pedal es controlada por el controlador PID y se limita a un rango de -50% a 100%. Cuando la posición del pedal es negativa, el automóvil está frenando.

Es útil tener un modelo del sistema al ajustar los coeficientes del controlador PID. Esto nos permite simular la respuesta del sistema. Para esto he implementado una clase Car en Python:

import numpy as npclass Car:    def __init__(self, masa, Crr, Cd, A, Fp):        self.masa = masa # [kg]        self.Crr = Crr # [-]        self.Cd = Cd # [-]        self.A = A # [m^2]        self.Fp = Fp # [N/%]        def obtener_aceleracion(self, pedal, velocidad):        # Constantes        rho = 1.225 # [kg/m^3]        g = 9.81 # [m/s^2]        # Fuerza de conducción        fuerza_de_conduccion = self.Fp * pedal        # Fuerza de resistencia al rodaje        fuerza_de_resistencia_al_rodaje = self.Crr * (self.masa * g)        # Fuerza de arrastre        fuerza_de_arrastre = 0.5 * rho * (velocidad ** 2) * self.Cd * self.A        aceleracion = (fuerza_de_conduccion - fuerza_de_resistencia_al_rodaje - fuerza_de_arrastre) / self.masa        return aceleracion        def simular(self, pasos, dt, velocidad, punto_de_consigna, controlador_pid):        pedal_s = np.zeros(pasos)        velocidad_s = np.zeros(pasos)        tiempo = np.zeros(pasos)        velocidad_s[0] = velocidad        for i in range(pasos - 1):            # Obtener posición del pedal [%]            pedal = controlador_pid.calcular(punto_de_consigna, velocidad, dt)            pedal = np.clip(pedal, -50, 100)            pedal_s[i] = pedal            # Obtener aceleración            aceleracion = self.obtener_aceleracion(pedal, velocidad)                        # Obtener velocidad            velocidad = velocidad_s[i] + aceleracion * dt            velocidad_s[i+1] = velocidad            tiempo[i+1] = tiempo[i] + dt                return pedal_s, velocidad_s, tiempo

La clase PIDController se implementa como:

class PIDController:    def __init__(self, Kp, Ki, Kd):        self.Kp = Kp        self.Ki = Ki        self.Kd = Kd        self.error_sum = 0        self.last_error = 0        def compute(self, setpoint, process_variable, dt):        error = setpoint - process_variable                # Término proporcional        P = self.Kp * error                # Término integral        self.error_sum += error * dt        I = self.Ki * self.error_sum                # Término derivativo        D = self.Kd * (error - self.last_error)        self.last_error = error                # Salida PID        output = P + I + D                return output

Tomar este enfoque de programación orientada a objetos facilita mucho la configuración y ejecución de múltiples simulaciones con diferentes ganancias de controlador PID, como debemos hacer al ejecutar el algoritmo de descenso de gradiente.

La clase GradientDescent se implementa como:

class GradientDescent:    def __init__(self, a, learning_rate, cost_function, a_min=None, a_max=None):        self.a = a        self.learning_rate = learning_rate        self.cost_function = cost_function        self.a_min = a_min        self.a_max = a_max        self.G = np.zeros([len(a), len(a)])        self.points = []        self.result = []        def grad(self, a):        h = 0.0000001        a_h = a + (np.eye(len(a)) * h)        cost_function_at_a = self.cost_function(a)        grad = []        for i in range(0, len(a)):            grad.append((self.cost_function(a_h[i]) - cost_function_at_a) / h)        grad = np.array(grad)        return grad        def update_a(self, learning_rate, grad):        if len(grad) == 1:            grad = grad[0]        self.a -= (learning_rate * grad)        if (self.a_min is not None) or (self.a_min is not None):            self.a = np.clip(self.a, self.a_min, self.a_max)        def update_G(self, grad):        self.G += np.outer(grad,grad.T)        def execute(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_a(self.learning_rate, grad)        def execute_adagrad(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_G(grad)            learning_rate = self.learning_rate * np.diag(self.G)**(-0.5)            self.update_a(learning_rate, grad)

El algoritmo se ejecuta durante un número especificado de iteraciones llamando a execute o execute_adagrad. El método execute_adagrad ejecuta una forma modificada de descenso de gradiente llamada AdaGrad (descenso de gradiente adaptativo).

AdaGrad tiene tasas de aprendizaje por parámetro que aumentan para parámetros dispersos y disminuyen para parámetros menos dispersos. La tasa de aprendizaje se actualiza después de cada iteración en función de una suma histórica de los gradientes al cuadrado.

Utilizaremos AdaGrad para optimizar las ganancias del controlador PID para el sistema de control de crucero del automóvil. Usando AdaGrad, la ecuación de actualización del descenso de gradiente se convierte en:

Paso de actualización del descenso de gradiente de AdaGrad

Ahora necesitamos definir nuestra función de costo. La función de costo debe tomar un vector de parámetros de entrada como entrada y devolver un solo número; el costo. El objetivo del control de crucero del automóvil es acelerar el automóvil hasta la velocidad objetivo con el mínimo sobrepaso, tiempo de asentamiento y error en estado estacionario. Hay muchas formas en las que podríamos definir la función de costo en función de este objetivo. Aquí la definiremos como la integral de la magnitud del error a lo largo del tiempo:

Función de costo del control de crucero del automóvil

Dado que nuestra función de costo es una integral, podemos visualizarla como el área bajo la curva de la magnitud del error. Esperamos ver que el área bajo la curva se reduzca a medida que nos acercamos al mínimo global. Programáticamente, la función de costo se define como:

def car_cost_function(a):    # Parámetros del automóvil    masa = 1000.0  # Masa del automóvil [kg]    Cd = 0.2  # Coeficiente de arrastre []    Crr = 0.02 # Resistencia a la rodadura []    A = 2.5 # Área frontal del automóvil [m^2]    Fp = 30 # Fuerza de conducción por posición del pedal [%]    # Parámetros del controlador PID    Kp = a[0]    Ki = a[1]    Kd = a[2]    # Parámetros de la simulación    dt = 0.1  # Paso de tiempo    tiempo_total = 60.0  # Tiempo total de simulación    n_pasos = int(tiempo_total / dt)    velocidad_inicial = 0.0  # Velocidad inicial del automóvil [m/s]    velocidad_objetivo = 20.0 # Velocidad objetivo del automóvil [m/s]    # Definir objetos Car y PIDController    automovil = Car(masa, Crr, Cd, A, Fp)    controlador_pid = PIDController(Kp, Ki, Kd)    # Ejecutar simulación    pedal_s, velocidad_s, tiempo = automovil.simulate(n_pasos, dt, velocidad_inicial, velocidad_objetivo, controlador_pid)    # Calcular costo    costo = np.trapz(np.absolute(velocidad_objetivo - velocidad_s), tiempo)    return costo

La función de costo incluye los parámetros de simulación. La simulación se ejecuta durante 60 segundos. Durante este tiempo, observamos la respuesta del sistema a un cambio escalón en el punto de consigna de 0 m/s a 20 m/s. Al integrar la magnitud del error a lo largo del tiempo, se calcula el costo para cada iteración.

Ahora, todo lo que queda por hacer es ejecutar la optimización. Comenzaremos con valores iniciales de Kp = 5.0, Ki = 1.0 y Kd = 0.0. Estos valores dan como resultado una respuesta estable y oscilante, con sobrepaso, que eventualmente converge al punto de consigna. A partir de este punto de partida, ejecutaremos el algoritmo de descenso de gradiente durante 500 iteraciones utilizando una tasa de aprendizaje base de 𝛾=0.1:

a = np.array([5.0, 1.0, 0.0])gradient_descent = GradientDescent(a, 0.1, car_cost_function, a_min=[0,0,0])gradient_descent.execute_adagrad(500)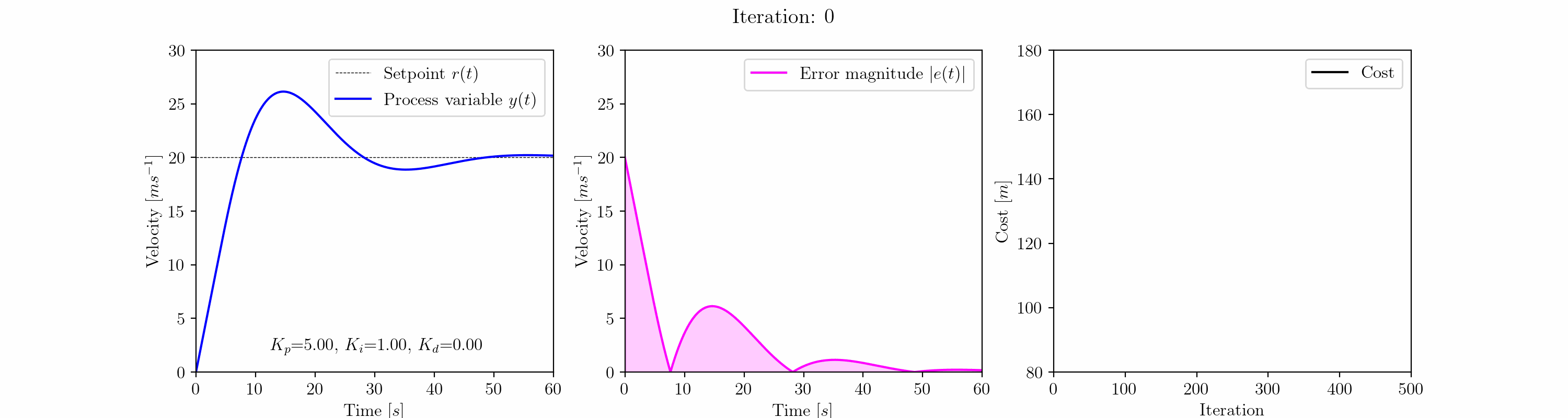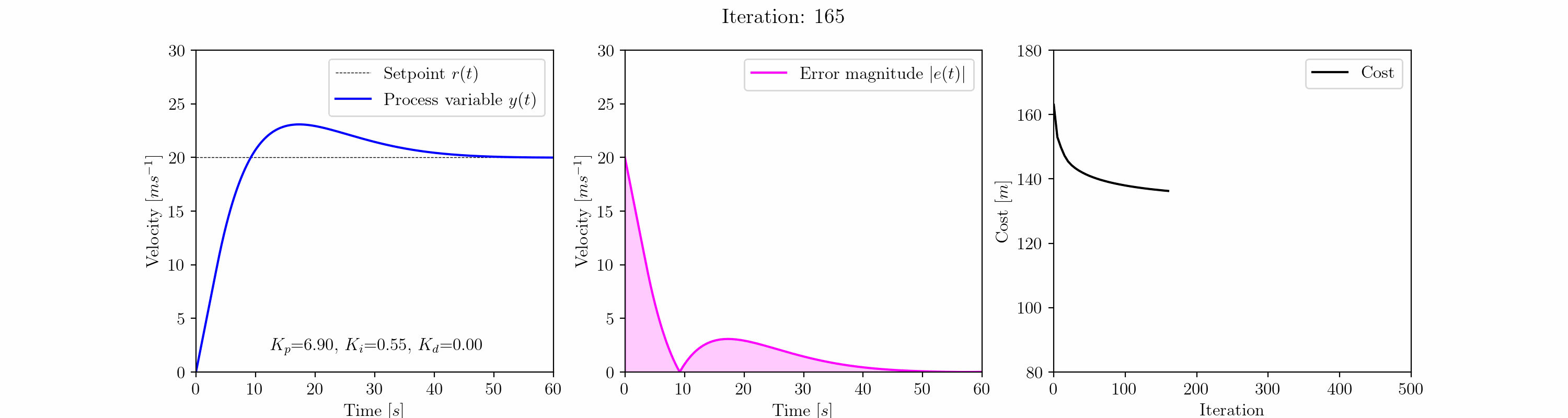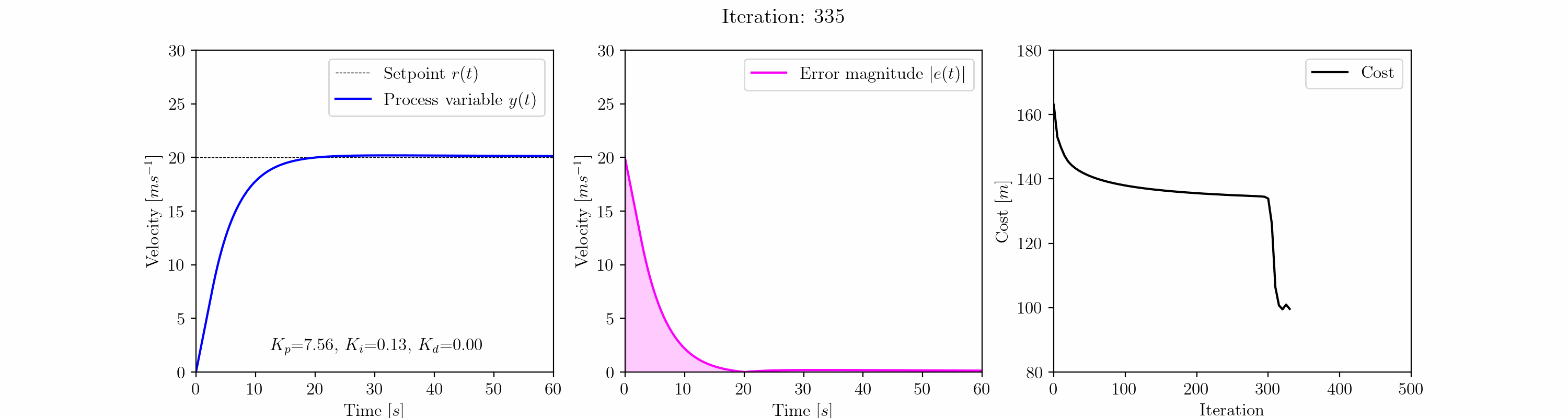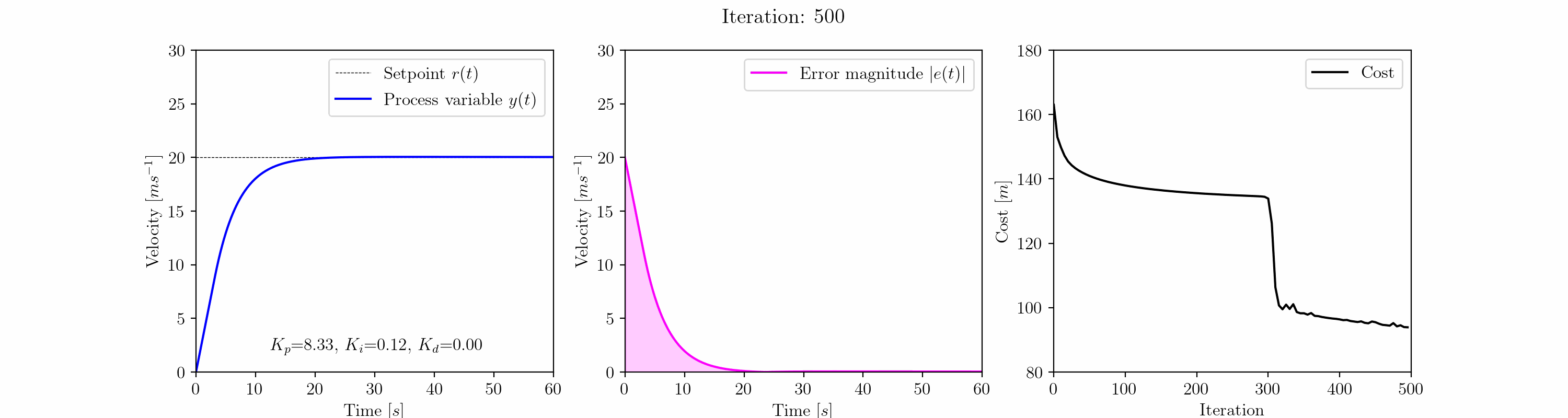

La gráfica animada de arriba muestra la evolución de la respuesta escalón del control de crucero del automóvil a medida que el algoritmo de descenso de gradiente ajusta los valores de ganancia Kp, Ki y Kd del controlador PID.

En la iteración 25, el algoritmo de descenso de gradiente ha eliminado la respuesta oscilatoria. Después de este punto, ocurre algo interesante. El algoritmo se adentra en un mínimo local caracterizado por un sobrepaso de ~ 3 m/s. Esto ocurre en la región de 6.0 < Kp < 7.5, Ki ~= 0.5, Kd = 0.0 y dura hasta la iteración 300.

Después de la iteración 300, el algoritmo sale del mínimo local para encontrar una respuesta más satisfactoria más cerca del mínimo global. La respuesta ahora se caracteriza por cero sobrepaso, tiempo de establecimiento rápido y error en estado estacionario cercano a cero.

Ejecutando el algoritmo de descenso de gradiente durante 500 iteraciones, obtenemos los valores optimizados de las ganancias del controlador PID; Kp = 8.33, Ki = 0.12 y Kd = 0.00.

La ganancia proporcional sigue aumentando constantemente. Ejecutando más iteraciones (no mostradas aquí), a medida que Kp aumenta gradualmente, encontramos que es posible lograr una reducción adicional en la función de costo, aunque este efecto se vuelve cada vez más marginal.

Resumen

Adoptando un método ampliamente utilizado para resolver problemas de aprendizaje automático y aprendizaje profundo, hemos optimizado con éxito las ganancias del controlador PID para un sistema de control de crucero de automóvil.

Comenzando con valores iniciales de Kp = 5.0, Ki = 1.0 y Kd = 0.0 y aplicando la forma de AdaGrad del algoritmo de descenso de gradiente, observamos cómo este sistema de baja dimensión primero se adentra en un mínimo local antes de encontrar eventualmente una respuesta más satisfactoria con cero sobrepaso, tiempo de establecimiento rápido y error en estado estacionario cercano a cero.

En este artículo, hemos visto cómo el descenso de gradiente puede ser una herramienta poderosa cuando se aplica a problemas clásicos de optimización en ingeniería. Más allá del ejemplo presentado aquí, el descenso de gradiente se puede utilizar para resolver otros problemas de ingeniería como la cinemática inversa en robótica, la optimización de topología y muchos más.

¿Tienes un problema de optimización al que crees que se le podría aplicar el descenso de gradiente? Déjame saber en los comentarios a continuación.

¿Disfrutaste leyendo este artículo?

Sigue y suscríbete para obtener más contenido como este, compártelo con tu red y prueba aplicar el descenso de gradiente a tus propios problemas de optimización.

Todas las imágenes, a menos que se indique lo contrario, son del autor.

Referencias

Web

[1] GitHub (2023), pid_controller_gradient_descent

[2] Wikipedia (2023), Método de Ziegler-Nichols (consultado el 10 de julio de 2023)

We will continue to update Zepes; if you have any questions or suggestions, please contact us!