Una guía para principiantes para comprender el rendimiento de las pruebas A/B a través de simulaciones de Monte Carlo

Guía para principiantes sobre pruebas A/B y simulaciones de Monte Carlo

Este tutorial explora cómo las covariables influyen en la precisión de las pruebas A/B en un experimento aleatorio. Una prueba A/B correctamente aleatorizada calcula el incremento comparando el resultado promedio en los grupos de tratamiento y control. Sin embargo, la influencia de características distintas al tratamiento en el resultado determina las propiedades estadísticas de la prueba A/B. Por ejemplo, omitir características influyentes en el cálculo del incremento de la prueba puede llevar a una estimación altamente imprecisa del incremento, incluso si converge al valor real a medida que aumenta el tamaño de la muestra.

Aprenderás qué es el RMSE, sesgo y tamaño de una prueba, y comprenderás el rendimiento de una prueba A/B a través de la generación de datos simulados y la ejecución de experimentos de Monte Carlo. Este tipo de trabajo es útil para entender cómo las propiedades del Proceso Generador de Datos (DGP) influyen en el rendimiento de las pruebas A/B y te ayudará a llevar este entendimiento a la ejecución de pruebas A/B en datos del mundo real. Primero, discutiremos algunas propiedades estadísticas básicas de un estimador.

Propiedades estadísticas de un estimador

Error Cuadrático Medio (RMSE)

RMSE (Error Cuadrático Medio): el RMSE es una medida frecuentemente utilizada de las diferencias entre los valores predichos por un modelo o un estimador y los valores observados. Es la raíz cuadrada del promedio de las diferencias al cuadrado entre la predicción y la observación real. La fórmula para el RMSE es:

RMSE = sqrt[(1/n) * Σ(observado – predicción)²]

• Crea tu propio asistente de análisis de datos con los agentes de Langchain
• ¿Puede la IA realmente ayudarte a pasar las entrevistas?
• AudioCraft de Meta Una Revolución en el Audio y la Música Generados por IA

El RMSE da un peso relativamente alto a los errores grandes debido a que se elevan al cuadrado antes de promediarlos, lo que significa que el RMSE debería ser más útil cuando los errores grandes son indeseables.

Sesgo

En estadística, el sesgo de un estimador es la diferencia entre el valor esperado de este estimador y el valor verdadero del parámetro estimado. Un estimador o regla de decisión con sesgo cero se llama insesgado; de lo contrario, se dice que el estimador tiene sesgo. En otras palabras, se produce un sesgo cuando un algoritmo aprende consistentemente algo incorrecto al no captar la relación subyacente precisa.

Por ejemplo, si intentas predecir los precios de las casas basándote en características de la casa, y tus predicciones están consistentemente $100,000 por debajo del precio real, tu modelo tiene sesgo.

Tamaño

En pruebas de hipótesis en estadística, el “tamaño de la prueba” se refiere al nivel de significancia de la prueba, a menudo representado por la letra griega α (alfa). El nivel de significancia, o tamaño de la prueba, es un umbral que una estadística de prueba debe superar para rechazar una hipótesis.

Representa la probabilidad de rechazar la hipótesis nula cuando esta es verdadera, lo cual es un tipo de error conocido como error de Tipo I o falso positivo.

Por ejemplo, si una prueba se establece a un nivel de significancia del 5% (α = 0.05), significa que hay un riesgo del 5% de rechazar la hipótesis nula cuando es verdadera. Este nivel, 0.05, es una elección común para α, aunque se pueden usar otros niveles, como 0.01 o 0.10, dependiendo del contexto y el campo de estudio.

Cuanto menor sea el tamaño de la prueba, más fuerte será la evidencia requerida para rechazar la hipótesis nula, lo que reduce la probabilidad de un error de Tipo I pero potencialmente aumenta la posibilidad de un error de Tipo II (no rechazar la hipótesis nula cuando es falsa). El equilibrio entre los errores de Tipo I y Tipo II es una consideración importante en el diseño de cualquier prueba estadística.

Tamaño empírico

El tamaño empírico en el contexto de las pruebas de hipótesis a través de simulaciones de Monte Carlo se refiere a la proporción de veces que la hipótesis nula es rechazada incorrectamente en las simulaciones cuando la hipótesis nula es verdadera. Esto es esencialmente una versión simulada de una tasa de error de Tipo I.

Aquí tienes un proceso general de cómo hacer esto:

1. Establece tu hipótesis nula y elige un nivel de significancia para tu prueba (por ejemplo, α = 0.05).

2. Genera un gran número de muestras bajo la suposición de que la hipótesis nula es verdadera. El número de muestras suele ser bastante grande, como 10,000 o 100,000, para asegurar la estabilidad de los resultados.

3. Para cada muestra, realiza la prueba de hipótesis y registra si se rechaza la hipótesis nula (puedes registrar esto como 1 para rechazo y 0 para no rechazo).

4. Calcula el tamaño empírico como la proporción de simulaciones en las que se rechazó la hipótesis nula. Esto estima la probabilidad de rechazar la hipótesis nula cuando es verdadera bajo el procedimiento de prueba dado.

El código a continuación muestra cómo implementar esto.

import numpy as np
from scipy.stats import ttest_1samp
import random
random.seed(10)

def calcular_tamaño_empírico(num_simulaciones: int, tamaño_muestra: int, media_verdadera: float, nivel_significancia: float) -> float:
    """
    Simula un conjunto de muestras y realiza una prueba de hipótesis en cada una, luego calcula el tamaño empírico.
    Parámetros:
    num_simulaciones (int): El número de simulaciones a ejecutar.
    tamaño_muestra (int): El tamaño de cada muestra simulada.
    media_verdadera (float): La media verdadera bajo la hipótesis nula.
    nivel_significancia (float): El nivel de significancia para las pruebas de hipótesis.
    Retorna:
    float: El tamaño empírico, o la proporción de pruebas en las que se rechazó la hipótesis nula.
    """
    import numpy as np
    from scipy.stats import ttest_1samp
    # Inicializar contador para rechazos de hipótesis nula
    rechazos = 0
    # Ejecutar simulaciones
    np.random.seed(0)  # para reproducibilidad
    for _ in range(num_simulaciones):
        muestra = np.random.normal(loc=media_verdadera, scale=1, size=tamaño_muestra)
        t_estadístico, valor_p = ttest_1samp(muestra, popmean=media_verdadera)
        if valor_p < nivel_significancia:
            rechazos += 1
    # Calcular tamaño empírico
    tamaño_empírico = rechazos / num_simulaciones
    return tamaño_empírico

calcular_tamaño_empírico(1000, 1000, 0, 0.05)

Para cada una de las 1000 simulaciones, se extrae una muestra aleatoria de tamaño 1000 de una distribución normal con media 0 y desviación estándar 1. Se realiza una prueba t de una muestra para verificar si la media de la muestra difiere significativamente de la media verdadera (0 en este caso). Si el valor p de la prueba es menor que el nivel de significancia (0.05), se rechaza la hipótesis nula.

El tamaño empírico se calcula como el número de veces que se rechaza la hipótesis nula (el número de falsos positivos) dividido por el número total de simulaciones. Este valor debería ser cercano al nivel de significancia nominal en una prueba bien calibrada. En este caso, la función devuelve el tamaño empírico, que da una idea de cuántas veces puede rechazar incorrectamente la hipótesis nula cuando en realidad es verdadera en aplicaciones del mundo real, asumiendo las mismas condiciones que en la simulación.

Debido a la variación aleatoria, el tamaño empírico puede no coincidir exactamente con el nivel de significancia nominal, pero deberían ser cercanos si el tamaño de la muestra es lo suficientemente grande y se cumplen las suposiciones de la prueba. Esta diferencia entre el tamaño empírico y el nominal es por qué se realizan estudios de simulación como este, para ver qué tan bien el tamaño nominal coincide con la realidad.

<h2

Experimentos sin covariables en el DGP

A continuación simulamos datos que siguen un DGP en el que el resultado solo es influenciado por el tratamiento y un error aleatorio.

y_i = tau*T_i+e_i

Si el resultado solo es influenciado por el tratamiento, las estimaciones del parámetro de efecto del tratamiento son precisas incluso para tamaños de muestra relativamente pequeños y convergen rápidamente al valor verdadero del parámetro a medida que aumenta el tamaño de la muestra. En el código a continuación, el valor del parámetro tau se establece en 2.

tau = 2corr = .5p = 10p0 = 0 # número de covariables utilizadas en el DGPNrange = range(10,1000,2) # bucle sobre los valores de N(nvalues,tauhats,sehats,lb,ub) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """Estimaciones del parámetro de efecto del tratamiento     para un experimento aleatorizado sin covariables"""fn_plot_with_ci(nvalues,tauhats,tau,lb,ub,caption)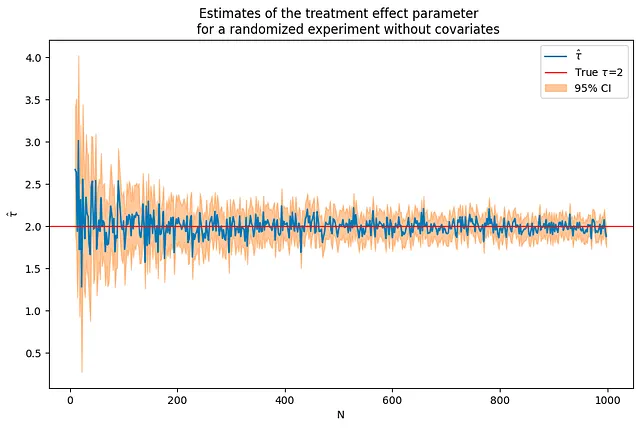

Para un tamaño de muestra seleccionado, verifique que esto es lo mismo que ejecutar una regresión con una intercepción.

Puede verificar que obtiene los mismos resultados ejecutando una regresión OLS del resultado sobre una intercepción y el tratamiento.

N = 100Yexp,T = fn_generate_data(tau,N,10,0,corr)Yt = Yexp[np.where(T==1)[0],:]Yc = Yexp[np.where(T==0)[0],:]tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)# n_values = n_values + [N]# tauhats = tauhats + [tauhat]lb = lb + [tauhat-1.96*se_tauhat]ub = ub + [tauhat+1.96*se_tauhat]print(f"Estimación del parámetro y error estándar obtenidos calculando la diferencia de medias:{tauhat:.5f},{se_tauhat:.5f}")const = np.ones([N,1])model = sm.OLS(Yexp,np.concatenate([T,const],axis = 1))res = model.fit()print(f"Estimación del parámetro y error estándar obtenidos ejecutando una regresión OLS con una intercepción:{res.params[0]:.5f},{ res.HC1_se[0]:.5f}")

Estimación del parámetro y error estándar obtenidos calculando la diferencia de medias:1.91756,0.21187Estimación del parámetro y error estándar obtenidos ejecutando una regresión OLS con una intercepción:1.91756,0.21187

Ejecutar iteraciones de Monte Carlo en R y calcular sesgo, RMSE y tamaño

Ahora ejecutará simulaciones de Monte Carlo en las que aumentará el tamaño de muestra al recorrer una lista de valores para el parámetroN. Calculará el RMSE, sesgo y tamaño empírico de la prueba para cada iteración.

Este script de Python realiza una simulación experimental para estudiar cómo el tamaño de muestra (N) afecta el sesgo, RMSE y tamaño del rendimiento de la prueba A/B cuando no se consideran covariables. Veámoslo paso a paso:

1. estDict = {} inicializa un diccionario vacío para almacenar los resultados experimentales.

2. R=2000 establece el número de repeticiones para el experimento en 2000.

3. for N in [10,50,100,500,1000] recorre diferentes tamaños de muestra.

4. Dentro de este bucle, tauhats=[], sehats=[] se inicializan como listas vacías para almacenar los efectos de tratamiento estimados tauhat y sus errores estándar correspondientes se_tauhat para cada experimento.

5. for r in tqdm(range(R)): recorre R experimentos, con una barra de progreso proporcionada por tqdm.

6. Yexp,T = fn_generate_data(tau,N,10,0,corr) genera datos sintéticos para cada experimento con un efecto de tratamiento predefinido tau, número de observaciones N, 10 covariables, sin covariables con coeficientes distintos de cero y una correlación predefinida.

7. Yt=Yexp[np.where(T==1)[0],:] y Yc=Yexp[np.where(T==0)[0],;] separan los datos sintéticos en grupos tratados y de control.

8. tauhat,se_tauhat=fn_tauhat_means(Yt,Yc) calcula la estimación del efecto del tratamiento y su error estándar.

9. tauhats=tauhats+[tauhat] y sehats=sehats+[se_tauhat] añaden la estimación del efecto del tratamiento y su error estándar a las listas correspondientes.

10. estDict[N]={‘tauhat':np.array(tauhats).reshape([len(tauahts),1]),’sehat':np.array(sehats).reshape([len(sehats),1])} almacena las estimaciones en el diccionario con el tamaño de la muestra como clave.

11. tau0 = tau*np.ones([R,1]) crea un arreglo de tamaño R con todos los elementos iguales al verdadero efecto del tratamiento.

12. Para cada tamaño de muestra en estDict, el script calcula e imprime el sesgo, RMSE y tamaño de la estimación del efecto del tratamiento utilizando la función fn_bias_rmse_size().

Como era de esperar, el sesgo y el RMSE disminuyen a medida que aumenta el tamaño de la muestra, y el tamaño se acerca al verdadero tamaño, 0.05.

estDict = {}R = 2000for N in [10,50,100,500,1000]:    tauhats = []    sehats = []    for r in tqdm(range(R)):        Yexp,T = fn_generate_data(tau,N,10,0,corr)        Yt = Yexp[np.where(T==1)[0],:]        Yc = Yexp[np.where(T==0)[0],:]        tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)        tauhats = tauhats + [tauhat]        sehats = sehats + [se_tauhat]    estDict[N] = {        'tauhat':np.array(tauhats).reshape([len(tauhats),1]),        'sehat':np.array(sehats).reshape([len(sehats),1])    }    tau0 = tau*np.ones([R,1])for N, results in estDict.items():    (bias,rmse,size) = fn_bias_rmse_size(tau0,results['tauhat'],                                         results['sehat'])    print(f'N={N}: bias={bias}, RMSE={rmse}, size={size}')

100%|██████████| 2000/2000 [00:00<00:00, 3182.81it/s]100%|██████████| 2000/2000 [00:00<00:00, 2729.99it/s]100%|██████████| 2000/2000 [00:00<00:00, 2238.62it/s]100%|██████████| 2000/2000 [00:04<00:00, 479.67it/s]100%|██████████| 2000/2000 [02:16<00:00, 14.67it/s]N=10: bias=0.038139125088721144, RMSE=0.6593256331782233, size=0.084N=50: bias=0.002694446014687934, RMSE=0.29664599979723183, size=0.0635N=100: bias=-0.0006785229668018156, RMSE=0.20246779253127453, size=0.0615N=500: bias=-0.0009696751953095926, RMSE=0.08985542730497854, size=0.062N=1000: bias=-0.0011137216061364087, RMSE=0.06156258265280801, size=0.047

Experimentos con covariables en la DGP

A continuación, se agregarán covariables a la DGP. Ahora, el resultado de interés depende no solo del tratamiento sino también de algunas otras variables X. El código a continuación simula datos con 50 covariables incluidas en la DGP. Utilizando los mismos tamaños de muestra y parámetro de efecto de tratamiento que en la simulación anterior sin covariables, puedes ver que esta vez las estimaciones son mucho más ruidosas, pero aún convergen a la solución correcta.

y_i = tau*T_i + beta*x_i + e_i

La gráfica a continuación compara las estimaciones de los dos DGPs, se puede observar cuánto más ruidosas son las estimaciones cuando se introducen covariables en el DGP.

tau = 2corr = .5p = 100p0 = 50 # número de covariables utilizadas en el DGPNrange = range(10,1000,2) # bucle sobre valores de N(nvalues_x,tauhats_x,sehats_x,lb_x,ub_x) = fn_run_experiments(tau,Nrange,p,p0,corr)caption = """Estimaciones del parámetro del efecto del tratamiento para un experimento aleatorizado con X's en el DGP pero sin X's incluidas en el estimador"""fn_plot_with_ci(nvalues_x,tauhats_x,tau,lb_x,ub_x,caption)# volver a ejecutar el experimento sin covariablesp0 = 0 # número de covariables utilizadas en el DGPNrange = range(10,1000,2) # bucle sobre valores de N(nvalues_x0,tauhats_x0,sehats_x0,lb_x0,ub_x0) = fn_run_experiments(tau,Nrange,p,p0,corr)fig = plt.figure(figsize = (10,6))plt.title("""Estimaciones del parámetro del efecto del tratamiento para un experimento aleatorizado con X's en el DGP pero sin X's incluidas en el estimador, acercamiento para grandes valores de N""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()fig = plt.figure(figsize = (10,6))plt.title("""Estimaciones del efecto del tratamiento del DGP con y sin covariables, acercamiento para grandes valores de N""")plt.plot(nvalues_x[400:],tauhats_x[400:],label = '$\hat{\\tau}^{(x)}$')plt.plot(nvalues_x[400:],tauhats_x0[400:],label = '$\hat{\\tau}$',color = 'green')plt.legend()

100%|██████████| 495/495 [00:41<00:00, 12.06it/s]100%|██████████| 495/495 [00:42<00:00, 11.70it/s]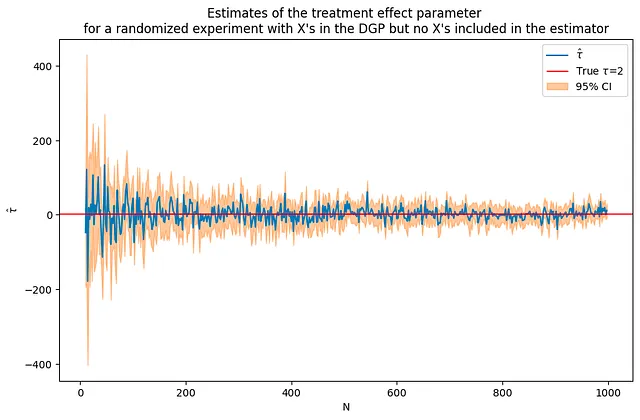

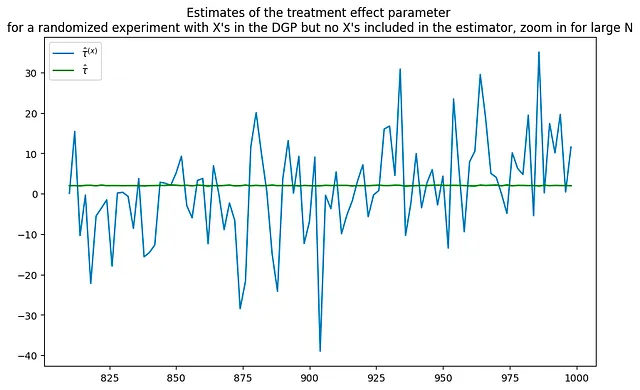
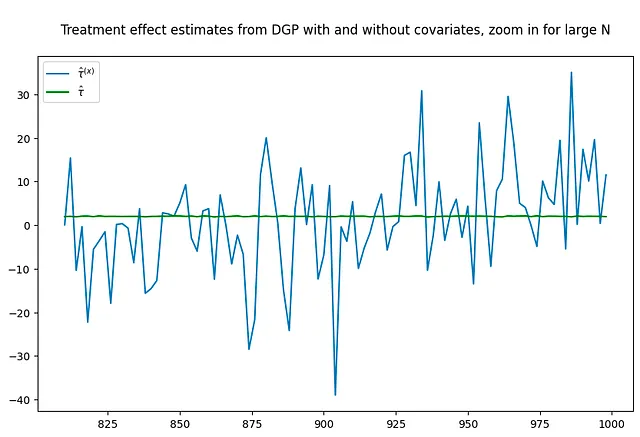
¿Repetir el experimento con una muestra mucho más grande resuelve el problema? No necesariamente. A pesar del aumento en el tamaño de la muestra, las estimaciones siguen siendo bastante ruidosas.

tau = 2corr = .5p = 100p0 = 50 # número de covariables utilizadas en el DGPNrange = range(1000,50000,10000) # bucle sobre valores de N(nvalues_x2,tauhats_x2,sehats_x2,lb_x2,ub_x2) = fn_run_experiments(tau,Nrange,p,p0,corr)fn_plot_with_ci(nvalues_x2,tauhats_x2,tau,lb_x2,ub_x2,caption)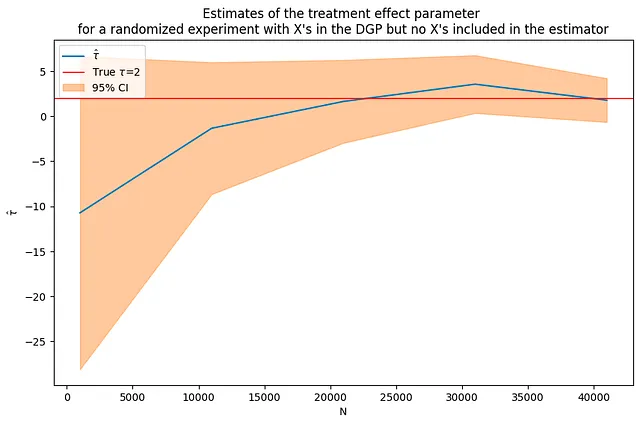

DGP con X — añadiendo covariables a la regresión

En esta parte, se utilizará el mismo DGP que antes:

y_i = tau*T_i + beta*x_i + e_i

Ahora, se incluirán estas covariables X en el modelo de regresión. Se encontrará que esto mejora significativamente la precisión de las estimaciones. Sin embargo, hay que tener en cuenta que esto es un poco “tramposo” — en este caso, se han incluido las covariables correctas desde el principio.

En un escenario del mundo real, es posible que no sepa qué covariables son las “correctas” para incluir, y puede ser necesario experimentar con diferentes modelos y covariables.

tau = 2corr = .5p = 100p0 = 50 # número de covariables utilizadas en el DGPrange = range(100,1000,2) # bucle sobre valores N# necesitamos empezar con más observaciones que pflagX = 1(nvalues2,tauhats2,sehats2,lb2,ub2) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX)caption = """Estimaciones del parámetro de efecto del tratamiento para un experimento aleatorio con X en el DGP, estimaciones obtenidas utilizando regresión con las X correctas"""fn_plot_with_ci(nvalues2,tauhats2,tau,lb2,ub2,caption)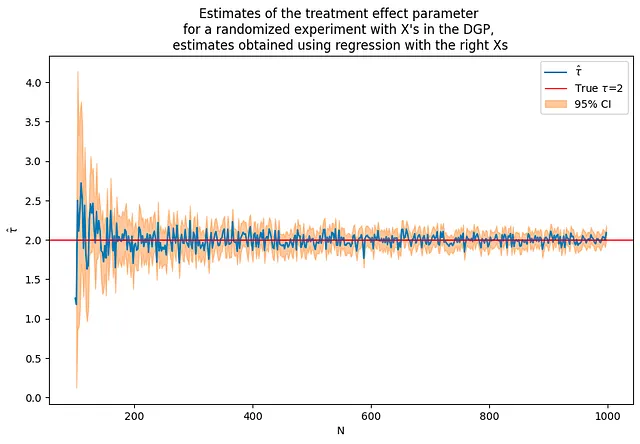

¿Qué sucede si utiliza algunas X que influyen en el resultado y algunas que no?

Esta sección examina la inclusión de algunas covariables relevantes y algunas irrelevantes en un modelo de regresión. Esto imita un escenario del mundo real donde puede no estar claro qué covariables influyen en el resultado.

Aunque se incluyen algunas variables no influyentes, se puede observar que la estimación general tiende a mejorar en comparación con el caso en que no se incluyeron covariables. Sin embargo, la inclusión de variables irrelevantes puede introducir algo de ruido e incertidumbre en las estimaciones, y es posible que no sean tan precisas como cuando solo se incluyeron las covariables relevantes.

En conclusión, comprender la influencia de las covariables en sus datos es esencial para mejorar la precisión y confiabilidad de los resultados de las pruebas A/B. Este tutorial explora las propiedades estadísticas de los estimadores como RMSE, sesgo y tamaño, y demuestra cómo se pueden estimar y comprender mediante simulaciones de Monte Carlo. También destaca el impacto de incluir covariables en el DGP y los modelos de regresión, enfatizando la importancia de una selección cuidadosa del modelo y pruebas de hipótesis en la práctica.

# Use el mismo DGP que antestau = 2corr = .5p = 100p0 = 50 # número de covariables utilizadas en el DGPa = 0.9b = 0.1Nrange = range(100,1000,2) # bucle sobre valores N# necesitamos empezar con más observaciones que pflagX = 2(nvalues3,tauhats3,sehats3,lb3,ub3) = fn_run_experiments(tau,Nrange,p,p0,corr,flagX,a,b)caption = f"""Estimaciones del parámetro de efecto del tratamiento para un experimento aleatorio con X en el DGP, estimaciones obtenidas utilizando regresión con el {100*a:.1f}% de las X correctas y el {100*b:.1f}% de las X irrelevantes"""fn_plot_with_ci(nvalues3,tauhats3,tau,lb3,ub3,caption)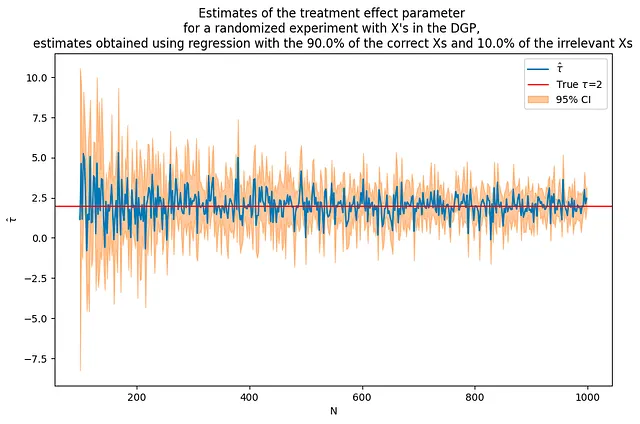

A menos que se indique lo contrario, todas las imágenes son del autor.

We will continue to update Zepes; if you have any questions or suggestions, please contact us!