El Reformador – Empujando los límites del modelado de lenguaje
'El Reformador Empujando los límites del modelado de lenguaje'
Cómo el Reformer utiliza menos de 8GB de RAM para entrenar en secuencias de medio millón de tokens
El modelo Reformer, presentado por Kitaev, Kaiser et al. (2020), es uno de los modelos de transformación más eficientes en memoria para el modelado de secuencias largas hasta la fecha.
Recientemente, el modelado de secuencias largas ha experimentado un aumento de interés, como se puede ver por las numerosas contribuciones de este año en solitario – Beltagy et al. (2020), Roy et al. (2020), Tay et al., Wang et al., por nombrar algunas. La motivación detrás del modelado de secuencias largas es que muchas tareas en PLN, como la sumarización, la respuesta a preguntas, requieren que el modelo procese secuencias de entrada más largas de las que los modelos, como BERT, son capaces de manejar. En tareas que requieren que el modelo procese una gran secuencia de entrada, los modelos de secuencia larga no tienen que recortar la secuencia de entrada para evitar el desbordamiento de memoria y, por lo tanto, se ha demostrado que superan a los modelos estándar “BERT”-like cf. Beltagy et al. (2020).
El Reformer empuja el límite del modelado de secuencias largas gracias a su capacidad para procesar hasta medio millón de tokens a la vez, como se muestra en esta demostración. Como comparación, un modelo convencional bert-base-uncased limita la longitud de entrada a solo 512 tokens. En Reformer, cada parte de la arquitectura estándar del transformador se rediseña para optimizar el requisito mínimo de memoria sin una caída significativa en el rendimiento.
- Modelos del Codificador-Decodificador basados en Transformadores
- Portando el sistema de traducción fairseq wmt19 a transformers
- Aprovechando los puntos de control de modelos de lenguaje pre-entrenados para modelos codificador-decodificador.
Las mejoras de memoria se pueden atribuir a 4 características que los autores de Reformer introdujeron en el mundo del transformador:
- Capa de Autoatención del Reformer – ¿Cómo implementar eficientemente la autoatención sin estar restringido a un contexto local?
- Capas de Feed Forward divididas en trozos – ¿Cómo obtener un mejor equilibrio entre el tiempo y la memoria para capas de feed forward grandes?
- Capas Residuales Reversibles – ¿Cómo reducir drásticamente el consumo de memoria en el entrenamiento mediante una arquitectura residual inteligente?
- Codificaciones posicionales axiales – ¿Cómo hacer que las codificaciones posicionales sean útiles para secuencias de entrada extremadamente grandes?
El objetivo de esta publicación es dar al lector una comprensión profunda de cada una de las cuatro características del Reformer mencionadas anteriormente. Si bien las explicaciones se centran en el Reformer, el lector debería tener una mejor intuición sobre en qué circunstancias cada una de las cuatro características puede ser efectiva para otros modelos de transformadores también. Las cuatro secciones están solo ligeramente conectadas, por lo que se pueden leer de forma individual.
El Reformer es parte de la biblioteca 🤗Transformers. Para todos los usuarios del Reformer, se recomienda leer esta publicación detallada para comprender mejor cómo funciona el modelo y cómo configurarlo correctamente. Todas las ecuaciones van acompañadas de su nombre equivalente en la configuración del Reformer, por ejemplo, config.<param_name>, para que el lector pueda relacionarse rápidamente con los documentos y el archivo de configuración oficiales.
Nota: Las codificaciones posicionales axiales no se explican en el documento oficial del Reformer, pero se utilizan ampliamente en el código oficial. Esta publicación proporciona la primera explicación detallada de las codificaciones posicionales axiales.
1. Capa de Autoatención del Reformer
El Reformer utiliza dos tipos de capas de autoatención especiales: capas de autoatención local y capas de autoatención con Local Sensitive Hashing (LSH).
Para introducir mejor estas nuevas capas de autoatención, haremos un breve resumen de la autoatención convencional tal como se introdujo en Vaswani et al. (2017).
Esta publicación utiliza la misma notación y colores que la popular publicación de blog The illustrated transformer, por lo que se recomienda encarecidamente al lector que lea primero este blog.
Importante: Si bien el Reformer fue introducido originalmente para la autoatención causal, también se puede utilizar perfectamente para la autoatención bidireccional. En esta publicación, se presenta la autoatención del Reformer para la autoatención bidireccional.
Resumen de la Autoatención Global
El núcleo de cada modelo Transformer es la capa de autoatención. Para resumir la capa de autoatención convencional, a la que nos referimos aquí como la capa de autoatención global, supongamos que aplicamos una capa de transformador a la secuencia de vectores de incrustación X = x 1 , … , x n, donde cada vector x i es de tamaño config.hidden_size, es decir, d h.
En resumen, una capa de autoatención global proyecta X \mathbf{X} X en las matrices de consulta, clave y valor Q , K , V \mathbf{Q}, \mathbf{K}, \mathbf{V} Q , K , V y calcula la salida Z \mathbf{Z} Z usando la operación softmax de la siguiente manera: Z = SelfAttn ( X ) = softmax ( Q K T ) V \mathbf{Z} = \text{SelfAttn}(\mathbf{X}) = \text{softmax}(\mathbf{Q}\mathbf{K}^T) \mathbf{V} Z = SelfAttn ( X ) = softmax ( Q K T ) V, donde Z \mathbf{Z} Z tiene una dimensión de d h × n d_h \times n d h × n (omitimos el factor de normalización de la clave y los pesos de autoatención W O \mathbf{W}^{O} W O por simplicidad). Para obtener más detalles sobre la operación completa del transformador, consulte el transformador ilustrado.
Visualmente, podemos ilustrar esta operación de la siguiente manera para n = 16 , d h = 3 n=16, d_h=3 n = 1 6 , d h = 3 :

Tenga en cuenta que para todas las visualizaciones se asume que batch_size y config.num_attention_heads son iguales a 1. Algunos vectores, como x 3 \mathbf{x_3} x 3 y su correspondiente vector de salida z 3 \mathbf{z_3} z 3 están marcados para poder explicar mejor la autoatención LSH más adelante. La lógica presentada puede ampliarse fácilmente para la autoatención de varias cabezas ( config.num_attention_{h}eads > 1). Se recomienda al lector que lea el transformador ilustrado como una referencia para la autoatención de varias cabezas.
Es importante recordar que para cada vector de salida z i \mathbf{z}_{i} z i , se procesa toda la secuencia de entrada X \mathbf{X} X. El tensor del producto punto interno Q K T \mathbf{Q}\mathbf{K}^T Q K T tiene una complejidad de memoria asintótica de O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) que generalmente representa el cuello de botella de memoria en un modelo de transformador.
Esta es también la razón por la cual bert-base-cased tiene un config.max_position_embedding_size de solo 512.
Autoatención local
La autoatención local es la solución obvia para reducir el cuello de botella de memoria O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) , lo que nos permite modelar secuencias más largas con un costo computacional reducido. En la autoatención local, la entrada X = X 1 : n = x 1 , … , x n \mathbf{X} = \mathbf{X}_{1:n} = \mathbf{x}_{1}, \ldots, \mathbf{x}_{n} X = X 1 : n = x 1 , … , x n se divide en n c n_{c} n c bloques: X = [ X 1 : l c , … , X ( n c − 1 ) ∗ l c : n c ∗ l c ] \mathbf{X} = \left[\mathbf{X}_{1:l_{c}}, \ldots, \mathbf{X}_{(n_{c} – 1) * l_{c} : n_{c} * l_{c}}\right] X = [ X 1 : l c , … , X ( n c − 1 ) ∗ l c : n c ∗ l c ] cada uno de longitud config.local_chunk_length , es decir, l c l_{c} l c , y posteriormente se aplica la autoatención global a cada bloque por separado.
Tomemos nuestra secuencia de entrada para n = 16 , d h = 3 n=16, d_h=3 n = 1 6 , d h = 3 nuevamente para su visualización:
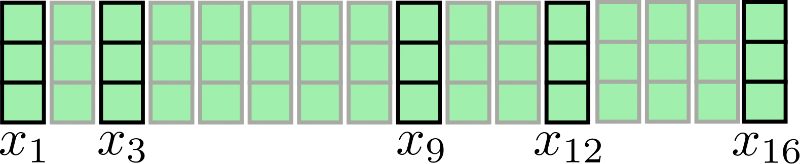
Suponiendo que lc = 4, nc = 4, la atención fragmentada puede ilustrarse de la siguiente manera:

Como se puede observar, la operación de atención se aplica a cada fragmento X1:4, X5:8, X9:12, X13:16 individualmente. La primera desventaja de esta arquitectura se vuelve evidente: algunos vectores de entrada no tienen acceso a su contexto inmediato, por ejemplo, x9 no tiene acceso a x8 y viceversa en nuestro ejemplo. Esto es problemático porque estos tokens no pueden aprender representaciones de palabras que tengan en cuenta su contexto inmediato.
Un remedio simple es aumentar cada fragmento con config.local_num_chunks_before, es decir, np fragmentos anteriores y config.local_num_chunks_after, es decir, na fragmentos siguientes, para que cada vector de entrada tenga al menos acceso a np vectores de entrada anteriores y na vectores de entrada siguientes. Esto también se puede entender como fragmentación con superposición, donde np y na definen la cantidad de superposición que tiene cada fragmento con todos los fragmentos anteriores y siguientes. Denominamos a esta autoatención local extendida de la siguiente manera:
Zloc = [Z1:lcloc, …, Z(nc – 1) * lc : nc * lcloc], con Zlc * (i – 1) + 1 : lc * i loc = SelfAttn(Xlc * (i – 1 – np) + 1 : lc * (i + na))[np * lc: -na * lc], ∀ i ∈ {1, …, nc}
Bien, esta fórmula parece bastante complicada. Hagámosla más fácil. En las capas de autoatención del Reformer, na generalmente se establece en 0 y np se establece en 1, así que escribamos la fórmula nuevamente para i = 1:
Z1:lcloc = SelfAttn(X – lc + 1 : lc)[lc:]
Observamos que tenemos una relación circular de modo que el primer segmento también puede atender al último segmento. Veamos nuevamente esta atención local ligeramente mejorada. Primero, aplicamos la auto-atención dentro de cada segmento con ventana y nos quedamos solo con el segmento central de salida.
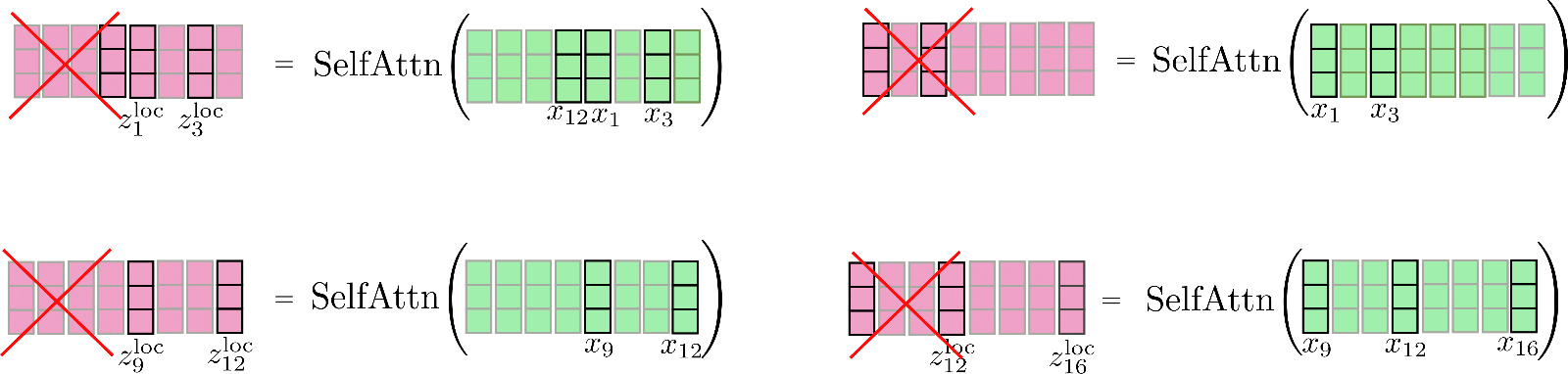
Finalmente, el resultado relevante se concatena a Z loc \mathbf{Z}^{\text{loc}} Z loc y se ve de la siguiente manera.
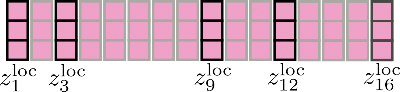
Es importante tener en cuenta que la auto-atención local se implementa de manera eficiente para que no se calcule y posteriormente se “descarte” ninguna salida, como se muestra aquí con fines ilustrativos mediante una cruz roja.
Es importante señalar aquí que ampliar los vectores de entrada para cada función de auto-atención segmentada permite que cada vector de salida individual z i \mathbf{z}_{i} z i de esta función de auto-atención aprenda mejores representaciones vectoriales. Por ejemplo, cada uno de los vectores de salida z 5 loc , z 6 loc , z 7 loc , z 8 loc \mathbf{z}_{5}^{\text{loc}}, \mathbf{z}_{6}^{\text{loc}}, \mathbf{z}_{7}^{\text{loc}}, \mathbf{z}_{8}^{\text{loc}} z 5 loc , z 6 loc , z 7 loc , z 8 loc puede tener en cuenta todos los vectores de entrada X 1 : 8 \mathbf{X}_{1:8} X 1 : 8 para aprender mejores representaciones.
La ganancia en el consumo de memoria es bastante obvia: la complejidad de memoria O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) se descompone para cada segmento individualmente, por lo que el consumo total de memoria asintótica se reduce a O ( n c ∗ l c 2 ) = O ( n ∗ l c ) \mathcal{O}(n_{c} * l_{c}^2) = \mathcal{O}(n * l_{c}) O ( n c ∗ l c 2 ) = O ( n ∗ l c ) .
Esta auto-atención local mejorada es mejor que la arquitectura de auto-atención local básica, pero aún tiene una desventaja importante en el sentido de que cada vector de entrada solo puede atender a un contexto local de tamaño predefinido. Para tareas de procesamiento del lenguaje natural que no requieren que el modelo transformer aprenda dependencias a largo plazo entre los vectores de entrada, que incluyen, por ejemplo, el reconocimiento de voz, el reconocimiento de entidades nombradas y la modelización del lenguaje causal de oraciones cortas, esto puede no ser un problema importante. Muchas tareas de procesamiento del lenguaje natural requieren que el modelo aprenda dependencias a largo plazo, por lo que la auto-atención local podría llevar a una degradación significativa del rendimiento, por ejemplo:
- Responder preguntas: el modelo debe aprender la relación entre los tokens de la pregunta y los tokens de respuesta relevantes, que probablemente no estarán en el mismo rango local
- Opción múltiple: el modelo debe comparar múltiples segmentos de tokens de respuesta entre sí, que generalmente están separados por una longitud significativa
- Resumen: el modelo debe aprender la relación entre una secuencia larga de tokens de contexto y una secuencia más corta de tokens de resumen, mientras que las relaciones relevantes entre el contexto y el resumen probablemente no pueden ser capturadas por la auto-atención local
- etc…
La auto-atención local por sí sola probablemente no es suficiente para que el modelo transformer aprenda las relaciones relevantes entre los vectores de entrada (tokens) entre sí.
Por lo tanto, Reformer utiliza adicionalmente una capa de auto-atención eficiente que aproxima la auto-atención global, llamada auto-atención LSH.
Auto-atención LSH
Bien, ahora que hemos entendido cómo funciona la auto-atención local, podemos abordar quizás la parte más innovadora de Reformer: Auto-atención por hashing sensible a la localidad (LSH).
La premisa de la auto-atención LSH es ser más o menos tan eficiente como la auto-atención local mientras se aproxima a la auto-atención global.
La auto-atención LSH se basa en el algoritmo LSH presentado en Andoni et al (2015), de ahí su nombre.
La idea detrás de la auto-atención LSH se basa en la idea de que si n n n es grande, la función softmax aplicada a los pesos del producto punto de atención Q K T \mathbf{Q}\mathbf{K}^T Q K T solo asigna muy pocos vectores de valor con valores significativamente mayores que 0 para cada vector de consulta.
Explicaremos esto con más detalle. Sea k i ∈ K = [ k 1 , … , k n ] T \mathbf{k}_{i} \in \mathbf{K} = \left[\mathbf{k}_1, \ldots, \mathbf{k}_n \right]^T k i ∈ K = [ k 1 , … , k n ] T y q i ∈ Q = [ q 1 , … , q n ] T \mathbf{q}_{i} \in \mathbf{Q} = \left[\mathbf{q}_1, \ldots, \mathbf{q}_n\right]^T q i ∈ Q = [ q 1 , … , q n ] T los vectores clave y consulta. Para cada q i \mathbf{q}_{i} q i , el cálculo softmax ( q i T K T ) \text{softmax}(\mathbf{q}_{i}^T \mathbf{K}^T) softmax ( q i T K T ) puede aproximarse utilizando solo aquellos vectores clave k j \mathbf{k}_{j} k j que tienen una alta similitud coseno con q i \mathbf{q}_{i} q i . Esto se debe a que la función softmax pone exponencialmente más peso en valores de entrada más grandes. Hasta aquí todo bien, el siguiente problema es encontrar eficientemente los vectores que tienen una alta similitud coseno con q i \mathbf{q}_{i} q i para todos los i i i.
Primero, los autores de Reformer notan que compartir las proyecciones de consulta y clave: Q = K \mathbf{Q} = \mathbf{K} Q = K no afecta el rendimiento de un modelo de transformador 1 {}^1 1 . Ahora, en lugar de tener que encontrar los vectores clave de alta similitud coseno para cada vector de consulta q i q_i q i , solo es necesario encontrar la similitud coseno de los vectores de consulta entre sí. Esto es importante porque hay una propiedad transitiva en la aproximación del producto punto del vector de consulta con el vector de consulta: si q i \mathbf{q}_{i} q i tiene una alta similitud coseno con los vectores de consulta q j \mathbf{q}_{j} q j y q k \mathbf{q}_{k} q k , entonces q j \mathbf{q}_{j} q j también tiene una alta similitud coseno con q k \mathbf{q}_{k} q k . Por lo tanto, los vectores de consulta se pueden agrupar en cubetas, de modo que todos los vectores de consulta que pertenezcan a la misma cubeta tengan una alta similitud coseno entre sí. Definamos C m C_{m} C m como el conjunto m-ésimo de índices de posición, de modo que sus vectores de consulta correspondientes estén en la misma cubeta: C m = { i ∣ s.t. q i ∈ mth cluster } C_{m} = \{ i | \text{ s.t. } \mathbf{q}_{i} \in \text{mth cluster}\} C m = { i ∣ s.t. q i ∈ mth cluster } y config.num_buckets, es decir, n b n_{b} n b , como el número de cubetas.
Para cada conjunto de índices C m C_{m} C m , la función softmax en la cubeta correspondiente de vectores de consulta softmax ( Q i ∈ C m Q i ∈ C m T ) \text{softmax}(\mathbf{Q}_{i \in C_{m}} \mathbf{Q}^T_{i \in C_{m}}) softmax ( Q i ∈ C m Q i ∈ C m T ) aproxima la función softmax de la auto-atención global con proyecciones compartidas de consulta y clave softmax ( q i T Q T ) \text{softmax}(\mathbf{q}_{i}^T \mathbf{Q}^T) softmax ( q i T Q T ) para todos los índices de posición i i i en C m C_{m} C m .
En segundo lugar, los autores utilizan el algoritmo LSH para agrupar los vectores de consulta en un número predefinido de cubetas n b n_{b} n b . El algoritmo LSH es una elección ideal aquí porque es muy eficiente y es una aproximación del algoritmo del vecino más cercano para la similitud coseno. Explicar el esquema LSH está fuera del alcance de esta nota, así que vamos a tener en cuenta que para cada vector q i \mathbf{q}_{i} q i , el algoritmo LSH atribuye su índice de posición i i i a una de las n b n_{b} n b cubetas predefinidas, es decir, LSH ( q i ) = m \text{LSH}(\mathbf{q}_{i}) = m LSH ( q i ) = m con i ∈ { 1 , … , n } i \in \{1, \ldots, n\} i ∈ { 1 , … , n } y m ∈ { 1 , … , n b } m \in \{1, \ldots, n_{b}\} m ∈ { 1 , … , n b }.
Visualmente, podemos ilustrar esto de la siguiente manera para nuestro ejemplo original:

Tercero, se puede observar que al agrupar todos los vectores de consulta en n b n_{b} n b cubetas, el conjunto correspondiente de índices C m C_{m} C m se puede usar para permutar los vectores de entrada x 1 , … , x n \mathbf{x}_1, \ldots, \mathbf{x}_n x 1 , … , x n en consecuencia 2 {}^2 2 de manera que la atención propia de consulta clave compartida se pueda aplicar por partes de manera similar a la atención local.
Aclaremos con nuestros vectores de entrada de ejemplo X = x 1 , . . . , x 16 \mathbf{X} = \mathbf{x}_1, …, \mathbf{x}_{16} X = x 1 , . . . , x 1 6 y supongamos config.num_buckets=4 y config.lsh_chunk_length = 4 . Mirando el gráfico de arriba, podemos ver que hemos asignado cada vector de consulta q 1 , … , q 16 \mathbf{q}_1, \ldots, \mathbf{q}_{16} q 1 , … , q 1 6 a uno de los grupos C 1 , C 2 , C 3 , C 4 \mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}, \mathcal{C}_{4} C 1 , C 2 , C 3 , C 4 . Si ahora ordenamos los vectores de entrada correspondientes x 1 , … , x 16 \mathbf{x}_1, \ldots, \mathbf{x}_{16} x 1 , … , x 1 6 en consecuencia, obtenemos la siguiente entrada permutada X ′ \mathbf{X’} X ′ :
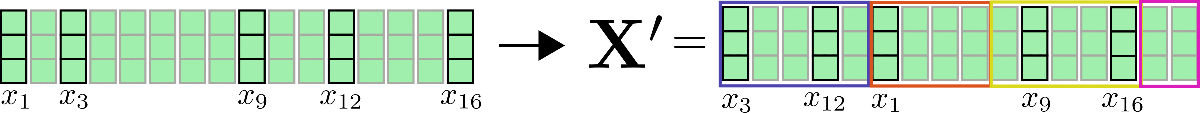
El mecanismo de autoatención debe aplicarse para cada grupo individualmente de manera que para cada grupo C m \mathcal{C}_m C m se calcule la siguiente salida: Z i ∈ C m LSH = SelfAttn Q = K ( X i ∈ C m ) \mathbf{Z}^{\text{LSH}}_{i \in \mathcal{C}_m} = \text{SelfAttn}_{\mathbf{Q}=\mathbf{K}}(\mathbf{X}_{i \in \mathcal{C}_m}) Z i ∈ C m LSH = SelfAttn Q = K ( X i ∈ C m ) .
Ilustremos esto nuevamente con nuestro ejemplo.
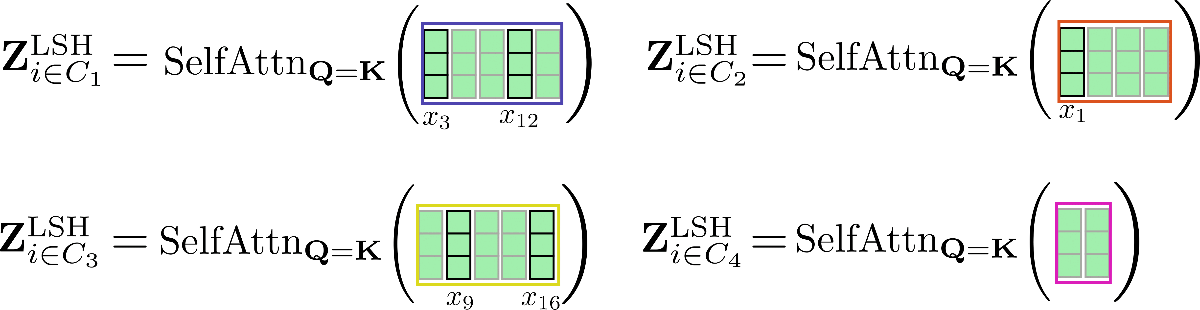
Como se puede ver, la función de autoatención opera en matrices de diferentes tamaños, lo cual no es óptimo para el agrupamiento eficiente en GPU y TPU.
Para superar este problema, la entrada permutada se puede dividir en fragmentos de la misma manera que se hace para la atención local, de manera que cada fragmento tenga un tamaño de config.lsh_chunk_length . Al dividir la entrada permutada, una cubeta podría dividirse en dos fragmentos diferentes. Para solucionar este problema, en la autoatención LSH cada fragmento se relaciona con su fragmento anterior config.lsh_num_chunks_before=1 además de sí mismo, de la misma manera que lo hace la autoatención local ( config.lsh_num_chunks_after generalmente se establece en 0). De esta manera, podemos estar seguros de que todos los vectores en una cubeta se relacionan entre sí con alta probabilidad 3 {}^3 3 .
En resumen, para todos los fragmentos k ∈ { 1 , … , n c } k \in \{1, \ldots, n_{c}\} k ∈ { 1 , … , n c } , la autoatención LSH se puede describir de la siguiente manera:
Z ′ l c ∗ k + 1 : l c ∗ ( k + 1 ) LSH = SelfAttn Q = K ( X ′ l c ∗ k + 1 ) : l c ∗ ( k + 1 ) ) [ l c : ] \mathbf{Z’}_{l_{c} * k + 1:l_{c} * (k + 1)}^{\text{LSH}} = \text{SelfAttn}_{\mathbf{Q} = \mathbf{K}}(\mathbf{X’}_{l_{c} * k + 1): l_{c} * (k + 1)})\left[l_{c}:\right] Z ′ l c ∗ k + 1 : l c ∗ ( k + 1 ) LSH = SelfAttn Q = K ( X ′ l c ∗ k + 1 ) : l c ∗ ( k + 1 ) ) [ l c : ]
con X ′ \mathbf{X’} X ′ y Z ′ \mathbf{Z’} Z ′ siendo los vectores de entrada y salida permutados según el algoritmo LSH. Suficientes fórmulas complicadas, vamos a ilustrar la auto-atención LSH.
Los vectores permutados X ′ \mathbf{X’} X ′ mostrados arriba se dividen en fragmentos y se aplica la auto-atención de consulta clave compartida a cada fragmento.
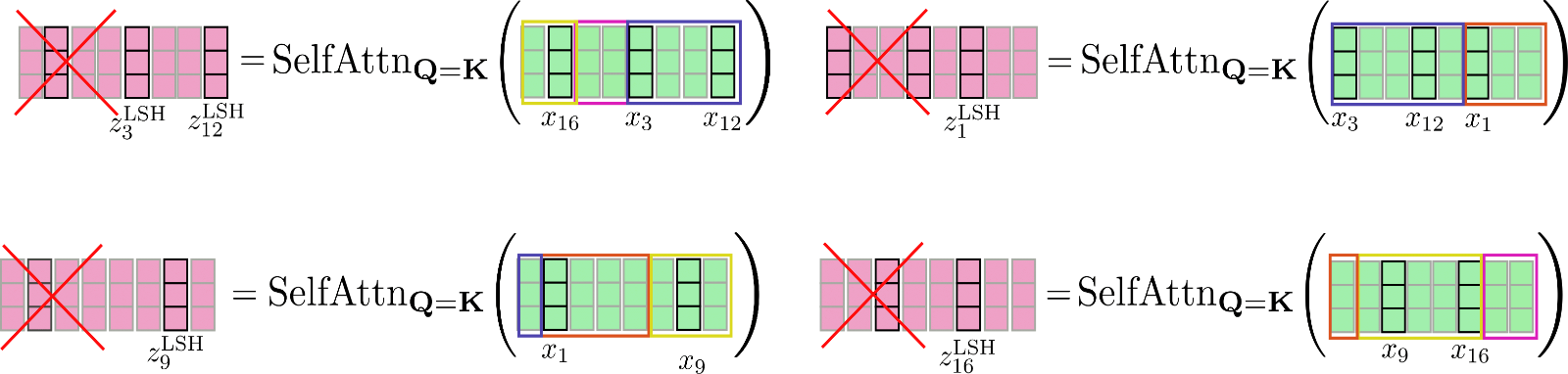
Finalmente, la salida Z ′ LSH \mathbf{Z’}^{\text{LSH}} Z ′ LSH se reordena a su permutación original.
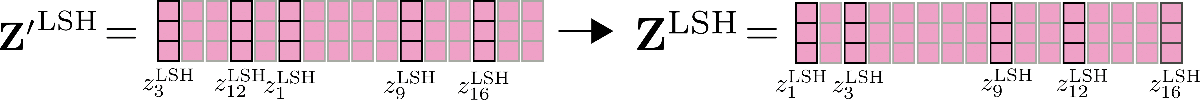
Otra característica importante a mencionar aquí es que la precisión de la auto-atención LSH se puede mejorar ejecutando la auto-atención LSH config.num_hashes, por ejemplo, n h n_{h} n h veces en paralelo, cada una con un hash LSH aleatorio diferente. Configurando config.num_hashes > 1, para cada posición de salida i i i, se calculan y fusionan múltiples vectores de salida z i LSH , 1 , … , z i LSH , n h \mathbf{z}^{\text{LSH}, 1}_{i}, \ldots, \mathbf{z}^{\text{LSH}, n_{h}}_{i} z i LSH , 1 , … , z i LSH , n h : z i LSH = ∑ k n h Z i LSH , k ∗ weight i k \mathbf{z}^{\text{LSH}}_{i} = \sum_k^{n_{h}} \mathbf{Z}^{\text{LSH}, k}_{i} * \text{weight}^k_i z i LSH = ∑ k n h Z i LSH , k ∗ weight i k . El peso i k \text{weight}^k_i peso i k representa la importancia de los vectores de salida z i LSH , k \mathbf{z}^{\text{LSH}, k}_{i} z i LSH , k de la ronda de hash k k k en comparación con las demás rondas de hash, y es exponencialmente proporcional al término de normalización de su cálculo softmax. La intuición detrás de esto es que si el vector de consulta correspondiente q i k \mathbf{q}_{i}^{k} q i k tiene una alta similitud coseno con todos los demás vectores de consulta en su fragmento respectivo, entonces el término de normalización softmax de este fragmento tiende a ser alto, por lo que los vectores de salida correspondientes q i k \mathbf{q}_{i}^{k} q i k deberían ser una mejor aproximación a la atención global y, por lo tanto, recibir más peso que los vectores de salida de las rondas de hash con un término de normalización softmax más bajo. Para más detalles, consulte el Apéndice A del artículo. Para nuestro ejemplo, la auto-atención LSH de múltiples rondas se puede ilustrar de la siguiente manera.
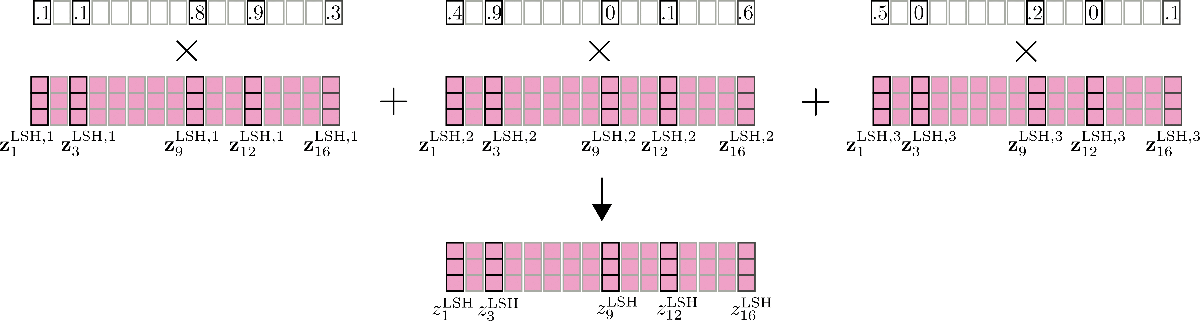
Genial. Eso es todo. Ahora sabemos cómo funciona la auto-atención LSH en Reformer.
En cuanto a la complejidad de memoria, ahora tenemos dos términos que compiten entre sí para ser el cuello de botella de memoria: el producto punto: O ( n h ∗ n c ∗ l c 2 ) = O ( n ∗ n h ∗ l c ) \mathcal{O}(n_{h} * n_{c} * l_{c}^2) = \mathcal{O}(n * n_{h} * l_{c}) O ( n h ∗ n c ∗ l c 2 ) = O ( n ∗ n h ∗ l c ) y la memoria requerida para la agrupación LSH: O ( n ∗ n h ∗ n b 2 ) \mathcal{O}(n * n_{h} * \frac{n_{b}}{2}) O ( n ∗ n h ∗ 2 n b ) con l c l_{c} l c siendo la longitud del fragmento. Debido a que para n n n grande, el número de grupos n b 2 \frac{n_{b}}{2} 2 n b crece mucho más rápido que la longitud del fragmento l c l_{c} l c , el usuario puede factorizar nuevamente el número de grupos config.num_buckets como se explica aquí.
Vamos a recapitular rápidamente lo que hemos revisado anteriormente:
- Queremos aproximar la atención global utilizando el conocimiento de que la operación softmax solo pone pesos significativos en unos pocos vectores clave.
- Si los vectores clave son iguales a los vectores de consulta, esto significa que para cada vector de consulta q i \mathbf{q}_{i} q i , el softmax solo pone peso significativo en otros vectores de consulta que son similares en cuanto a la similitud del coseno.
- Esta relación funciona en ambos sentidos, lo que significa que si q j \mathbf{q}_{j} q j es similar a q i \mathbf{q}_{i} q i , entonces q j \mathbf{q}_{j} q j también es similar a q i \mathbf{q}_{i} q i , de modo que podemos hacer un agrupamiento global antes de aplicar la auto-atención en una entrada permutada.
- Aplicamos auto-atención local en la entrada permutada y reordenamos la salida a su permutación original.
1 {}^{1} 1 Los autores realizaron algunos experimentos preliminares que confirman que la auto-atención compartida de consulta clave funciona más o menos igual de bien que la auto-atención estándar.
2 {}^{2} 2 Para ser más exactos, los vectores de consulta dentro de un cubo se ordenan según su orden original. Esto significa que si, por ejemplo, los vectores q 1 , q 3 , q 7 \mathbf{q}_1, \mathbf{q}_3, \mathbf{q}_7 q 1 , q 3 , q 7 se asignan a todos al cubo 2, el orden de los vectores en el cubo 2 seguiría siendo q 1 \mathbf{q}_1 q 1 , seguido de q 3 \mathbf{q}_3 q 3 y q 7 \mathbf{q}_7 q 7 .
3 {}^3 3 En una nota aparte, cabe mencionar que los autores colocan una máscara en el vector de consulta q i \mathbf{q}_{i} q i para evitar que el vector se atienda a sí mismo. Debido a que la similitud del coseno de un vector consigo mismo siempre será igual o mayor que la similitud del coseno con otros vectores, se desaconseja enérgicamente que los vectores de consulta en la auto-atención compartida de consulta clave se atiendan a sí mismos.
Referencia
Recientemente se añadieron herramientas de referencia a Transformers – ver aquí para una explicación más detallada.
Para mostrar cuánta memoria se puede ahorrar utilizando la auto-atención “local” + “LSH”, se realiza una referencia del modelo Reformer google/reformer-enwik8 para diferentes longitud_tramo_autoatencion_local y longitud_tramo_autoatencion_lsh . La configuración predeterminada y el uso del modelo google/reformer-enwik8 se pueden consultar con más detalle aquí .
Primero, hagamos algunas importaciones e instalaciones necesarias.
#@title Instalaciones e importaciones
# Instalaciones con pip
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArgumentsEn primer lugar, comparemos el uso de memoria del modelo Reformer utilizando la auto-atención global. Esto se puede lograr estableciendo longitud_tramo_autoatencion_lsh = longitud_tramo_autoatencion_local = 8192 para que, para todas las secuencias de entrada menores o iguales a 8192, el modelo cambie automáticamente a la auto-atención global.
config = ReformerConfig.from_pretrained("google/reformer-enwik8", longitud_tramo_autoatencion_lsh=16386, longitud_tramo_autoatencion_local=16386, numero_tramos_lsh_antes=0, numero_tramos_local_antes=0)
args_referencia = PyTorchBenchmarkArguments(longitudes_secuencia=[2048, 4096, 8192, 16386], tamaños_lote=[1], modelos=["Reformer"], sin_velocidad=True, sin_impresion_entorno=True)
referencia = PyTorchBenchmark(configs=[config], args=args_referencia)
resultado = referencia.run()
HBox(children=(FloatProgress(value=0.0, description='Descargando', max=1279.0, style=ProgressStyle(description…
1 / 1
No cabe en la GPU. Memoria CUDA agotada. Se intentó asignar 2.00 GiB (GPU 0; capacidad total de 11.17 GiB; 8.87 GiB ya asignados; 1.92 GiB libres; 8.88 GiB reservados en total por PyTorch)
==================== INFERENCIA - MEMORIA - RESULTADO ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Lote Longitud de Secuencia Memoria en MB
--------------------------------------------------------------------------------
Reformer 1 2048 1465
Reformer 1 4096 2757
Reformer 1 8192 7893
Reformer 1 16386 N/A
--------------------------------------------------------------------------------Cuanto más larga sea la secuencia de entrada, más visible es la relación cuadrática O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) entre la secuencia de entrada y el uso máximo de memoria. Como se puede ver, en la práctica se requeriría una secuencia de entrada mucho más larga para observar claramente que duplicar la secuencia de entrada cuadruplica el uso máximo de memoria.
Para esto, un modelo google/reformer-enwik8 utilizando atención global, una longitud de secuencia superior a 16K resulta en un desbordamiento de memoria.
Ahora, activemos la atención local y LSH utilizando los parámetros predeterminados del modelo.
config = ReformerConfig.from_pretrained("google/reformer-enwik8")
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16384, 32768, 65436], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()
1 / 1
No cabe en la GPU. CUDA se quedó sin memoria. Se intentó asignar 2.00 GiB (GPU 0; capacidad total de 11.17 GiB; 7.85 GiB ya asignados; 1.74 GiB libres; 9.06 GiB reservados en total por PyTorch)
No cabe en la GPU. CUDA se quedó sin memoria. Se intentó asignar 4.00 GiB (GPU 0; capacidad total de 11.17 GiB; 6.56 GiB ya asignados; 3.99 GiB libres; 6.81 GiB reservados en total por PyTorch)
==================== INFERENCIA - MEMORIA - RESULTADO ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Batch Longitud de la Secuencia Memoria en MB
--------------------------------------------------------------------------------
Reformer 1 2048 1785
Reformer 1 4096 2621
Reformer 1 8192 4281
Reformer 1 16384 7607
Reformer 1 32768 N/A
Reformer 1 65436 N/A
--------------------------------------------------------------------------------Como era de esperar, el uso de la atención local y LSH es mucho más eficiente en cuanto a la memoria para secuencias de entrada más largas, de modo que el modelo se queda sin memoria solo con 16K tokens para una GPU de 11GB de RAM en esta notebook.
2. Capas de Avance de Chunked
Los modelos basados en Transformer a menudo utilizan capas de avance de gran tamaño después de la capa de autoatención en paralelo. De esta manera, esta capa puede ocupar una cantidad significativa de la memoria general y a veces incluso representar el cuello de botella de la memoria de un modelo. Introducido por primera vez en el artículo de Reformer, el avance de chunking es una técnica que permite intercambiar una mejor utilización de la memoria por un aumento en el tiempo de ejecución.
Capa de Avance de Chunked en Reformer
En Reformer, la capa de autoatención local, o LSH, suele ir seguida de una conexión residual, que luego define la primera parte en un bloque del transformador . Para obtener más detalles al respecto, consulte este blog .
La salida de la primera parte del bloque del transformador , llamada salida de autoatención normalizada, se puede escribir como Z ‾ = Z + X \mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X} Z = Z + X , siendo Z \mathbf{Z} Z ya sea Z LSH \mathbf{Z}^{\text{LSH}} Z LSH o Z loc \mathbf{Z}^\text{loc} Z loc en Reformer.
Para nuestra entrada de ejemplo x 1 , … , x 16 \mathbf{x}_1, \ldots, \mathbf{x}_{16} x 1 , … , x 1 6 , ilustramos la salida de autoatención normalizada de la siguiente manera.

Ahora, la segunda parte de un bloque del transformador generalmente consta de dos capas de avance de chunked 1 ^{1} 1 , definidas como Linear int ( … ) \text{Linear}_{\text{int}}(\ldots) Linear int ( … ) que procesa Z ‾ \mathbf{\overline{Z}} Z , a una salida intermedia Y int \mathbf{Y}_{\text{int}} Y int y Linear out ( … ) \text{Linear}_{\text{out}}(\ldots) Linear out ( … ) que procesa la salida intermedia a la salida Y out \mathbf{Y}_{\text{out}} Y out . Las dos capas de avance de chunked se pueden definir por
Y out = Salida lineal ( Y int ) = Salida lineal ( Intermedia lineal ( Z ‾ ) ) . \mathbf{Y}_{\text{out}} = \text{Salida lineal}(\mathbf{Y}_\text{int}) = \text{Salida lineal}(\text{Intermedia lineal}(\mathbf{\overline{Z}})). Y out = Salida lineal ( Y int ) = Salida lineal ( Intermedia lineal ( Z ) ) .
Es importante recordar en este punto que matemáticamente la salida de una capa de avance hacia adelante en la posición y out , i \mathbf{y}_{\text{out}, i} y out , i solo depende de la entrada en esta posición y ‾ i \mathbf{\overline{y}}_{i} y i . En contraste con la capa de autoatención, cada salida y out , i \mathbf{y}_{\text{out}, i} y out , i es completamente independiente de todas las entradas y ‾ j ≠ i \mathbf{\overline{y}}_{j \ne i} y j = i de diferentes posiciones.
Ilustremos las capas de avance hacia adelante para z ‾ 1 , … , z ‾ 16 \mathbf{\overline{z}}_1, \ldots, \mathbf{\overline{z}}_{16} z 1 , … , z 1 6 .
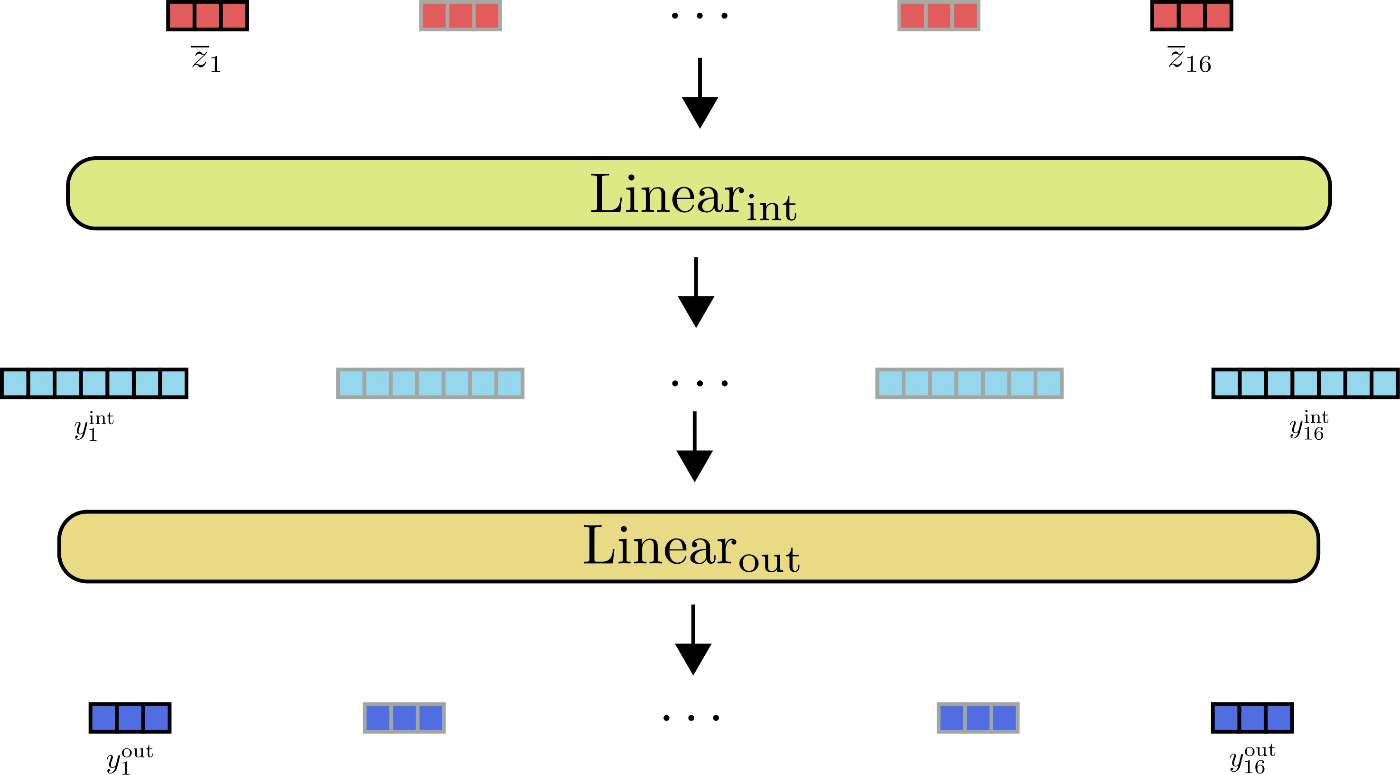
Como se puede ver en la ilustración, todos los vectores de entrada z ‾ i \mathbf{\overline{z}}_{i} z i son procesados por la misma capa de avance hacia adelante en paralelo.
Se vuelve interesante cuando se observan las dimensiones de salida de las capas de avance hacia adelante. En Reformer, la dimensión de salida de Linear int \text{Linear}_{\text{int}} Linear int se define como config.feed_forward_size , por ejemplo, d f d_{f} d f , y la dimensión de salida de Linear out \text{Linear}_{\text{out}} Linear out se define como config.hidden_size , es decir, d h d_{h} d h .
Los autores de Reformer observaron que en un modelo de transformer, la dimensión intermedia d f d_{f} d f tiende a ser mucho más grande que la dimensión de salida 2 ^{2} 2 d h d_{h} d h . Esto significa que el tensor Y int \mathbf{\mathbf{Y}}_\text{int} Y int de dimensión d f × n d_{f} \times n d f × n asigna una cantidad significativa de la memoria total e incluso puede convertirse en un cuello de botella de memoria.
Para tener una mejor idea de las diferencias en las dimensiones, vamos a representar las matrices Y int \mathbf{Y}_\text{int} Y int y Y out \mathbf{Y}_\text{out} Y out para nuestro ejemplo.
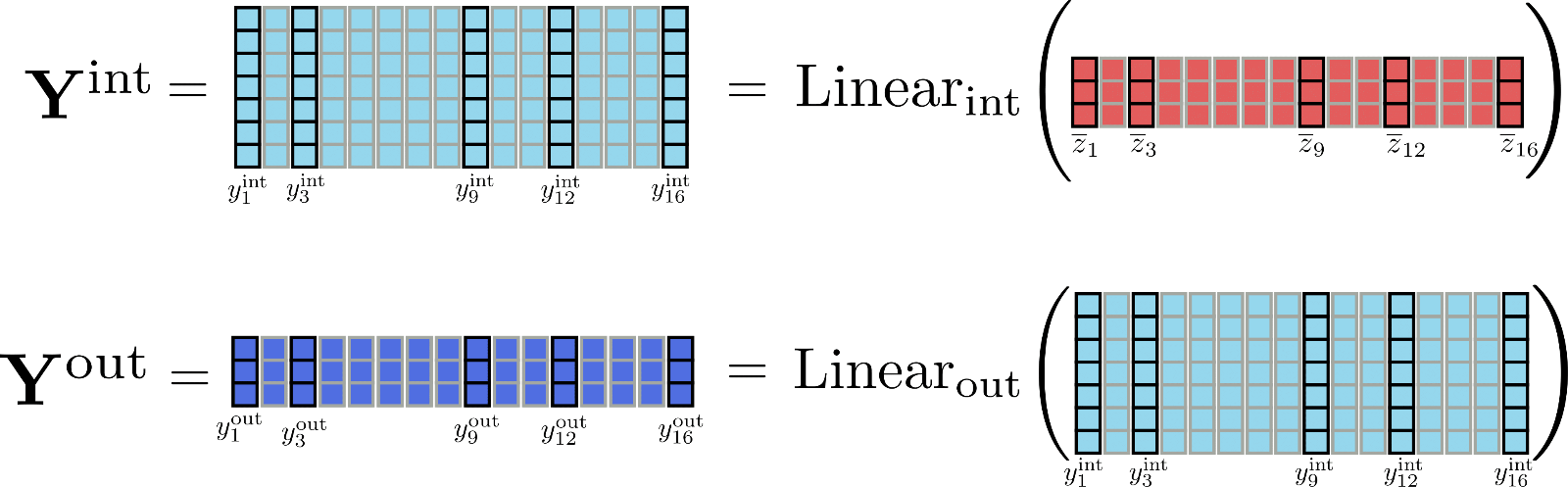
Es bastante evidente que el tensor Y int \mathbf{Y}_\text{int} Y int ocupa mucha más memoria ( d f d h × n \frac{d_{f}}{d_{h}} \times n d h d f × n exactamente) que Y out \mathbf{Y}_{\text{out}} Y out . Pero, ¿es necesario calcular la matriz intermedia completa Y int \mathbf{Y}_\text{int} Y int ? En realidad, no es necesario, porque lo relevante es solo la matriz de salida Y out \mathbf{Y}_\text{out} Y out . Para intercambiar memoria por velocidad, se puede dividir el cálculo de las capas lineales para procesar solo un fragmento a la vez. Definiendo config.chunk_size_feed_forward como c f c_{f} c f , las capas lineales fragmentadas se definen como Y out = [ Y out , 1 : c f , … , Y out , ( n − c f ) : n ] \mathbf{Y}_{\text{out}} = \left[\mathbf{Y}_{\text{out}, 1: c_{f}}, \ldots, \mathbf{Y}_{\text{out}, (n – c_{f}): n}\right] Y out = [ Y out , 1 : c f , … , Y out , ( n − c f ) : n ] donde Y out , ( c f ∗ i ) : ( i ∗ c f + i ) = Salida lineal ( Intermedia lineal ( Z ‾ ( c f ∗ i ) : ( i ∗ c f + i ) ) ) \mathbf{Y}_{\text{out}, (c_{f} * i): (i * c_{f} + i)} = \text{Salida lineal}(\text{Intermedia lineal}(\mathbf{\overline{Z}}_{(c_{f} * i): (i * c_{f} + i)})) Y out , ( c f ∗ i ) : ( i ∗ c f + i ) = Salida lineal ( Intermedia lineal ( Z ( c f ∗ i ) : ( i ∗ c f + i ) ) ) . En la práctica, esto significa que la salida se calcula incrementalmente y se concatena para evitar tener que almacenar todo el tensor intermedio Y int \mathbf{Y}_{\text{int}} Y int en la memoria.
Suponiendo c f = 1 para nuestro ejemplo, podemos ilustrar el cálculo incremental de la salida para la posición i = 9 de la siguiente manera.
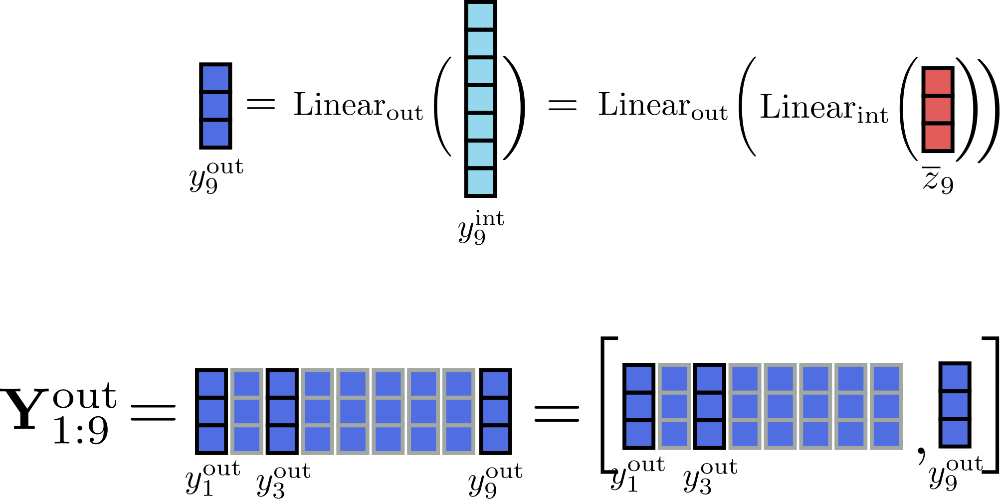
Al procesar las entradas en fragmentos de tamaño 1, los únicos tensores que deben almacenarse en memoria al mismo tiempo son Y out \mathbf{Y}_\text{out} Y out de un tamaño máximo de 16 × d h 16 \times d_{h} 1 6 × d h , y int , i \mathbf{y}_{\text{int}, i} y int , i de tamaño d f d_{f} d f y la entrada Z ‾ \mathbf{\overline{Z}} Z de tamaño 16 × d h 16 \times d_{h} 1 6 × d h , con d h d_{h} d h siendo config.hidden_size 3 ^{3} 3 .
Finalmente, es importante recordar que las capas lineales fragmentadas producen una salida matemáticamente equivalente a las capas lineales convencionales y, por lo tanto, se pueden aplicar a todas las capas lineales del transformador. El uso de config.chunk_size_feed_forward permite un mejor equilibrio entre memoria y velocidad en ciertos casos de uso.
1 {}^1 1 Para una explicación más sencilla, de momento se omite la capa de normalización de capa que normalmente se aplica a Z ‾ \mathbf{\overline{Z}} Z antes de ser procesada por las capas de avance feed forward.
2 {}^2 2 En bert-base-uncased , por ejemplo, la dimensión intermedia d f d_{f} d f es cuatro veces más grande que la dimensión de salida d h d_{h} d h .
3 {}^3 3 Como recordatorio, se asume que la salida config.num_attention_heads es 1 por claridad e ilustración en este cuaderno, de modo que se puede suponer que la salida de las capas de autoatención tiene un tamaño de config.hidden_size .
Más información sobre las capas lineales / feed forward fragmentadas se puede encontrar también aquí en la documentación de 🤗Transformers.
Benchmarks
Probemos cuánta memoria se puede ahorrar al utilizar capas feed forward fragmentadas.
#@title Instalaciones e importaciones
# pip install
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments
Building wheel for transformers (setup.py) ... [?25l[?25hdonePrimero, comparemos el modelo predeterminado google/reformer-enwik8 sin capas feed forward fragmentadas con el que tiene capas feed forward fragmentadas.
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8") # sin fragmentos
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1) # fragmentos de avance feed forward
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
No cabe en la GPU. CUDA sin memoria. Se intentó asignar 2.00 GiB (GPU 0; capacidad total de 11.17 GiB; 7.85 GiB ya asignados; 1.74 GiB libres; 9.06 GiB reservados en total por PyTorch)
2 / 2
No cabe en la GPU. CUDA sin memoria. Se intentó asignar 2.00 GiB (GPU 0; capacidad total de 11.17 GiB; 7.85 GiB ya asignados; 1.24 GiB libres; 9.56 GiB reservados en total por PyTorch)
==================== INFERENCIA - MEMORIA - RESULTADO ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Lote Longitud de Seq Memoria en MB
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 4281
Reformer-No-Chunk 8 2048 7607
Reformer-No-Chunk 8 4096 N/A
Reformer-Chunk 8 1024 4309
Reformer-Chunk 8 2048 7669
Reformer-Chunk 8 4096 N/A
--------------------------------------------------------------------------------Interesante, las capas de alimentación hacia adelante fragmentadas no parecen ayudar aquí en absoluto. La razón es que config.feed_forward_size no es lo suficientemente grande como para marcar una diferencia real. Solo en longitudes de secuencia más largas de 4096, se puede observar una ligera disminución en el uso de memoria.
Veamos qué sucede con el pico de uso de memoria si aumentamos el tamaño de la capa de alimentación hacia adelante en un factor de 4 y reducimos el número de cabezas de atención también en un factor de 4 para que la capa de alimentación hacia adelante se convierta en el cuello de botella de la memoria.
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=0, num_attention_{h}eads=2, feed_forward_size=16384) # sin fragmentar
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1, num_attention_{h}eads=2, feed_forward_size=16384) # fragmento de alimentación hacia adelante
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== INFERENCIA - MEMORIA - RESULTADO ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Lote Longitud de la Secuencia Memoria en MB
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 3743
Reformer-No-Chunk 8 2048 5539
Reformer-No-Chunk 8 4096 9087
Reformer-Chunk 8 1024 2973
Reformer-Chunk 8 2048 3999
Reformer-Chunk 8 4096 6011
--------------------------------------------------------------------------------Ahora se puede observar una clara disminución en el uso máximo de memoria para secuencias de entrada más largas. En conclusión, se debe tener en cuenta que las capas de alimentación hacia adelante fragmentadas solo tienen sentido para modelos que tienen pocas cabezas de atención y capas de alimentación hacia adelante grandes.
3. Capas Residuales Reversibles
Las capas residuales reversibles se introdujeron por primera vez en N. Gomez et al y se utilizan para reducir el consumo de memoria al entrenar el popular modelo ResNet. Matemáticamente, las capas residuales reversibles son ligeramente diferentes a las capas residuales “reales”, pero no requieren que las activaciones se guarden durante el paso hacia adelante, lo que puede reducir drásticamente el consumo de memoria para el entrenamiento.
Capas Residuales Reversibles en Reformer
Comencemos investigando por qué el entrenamiento de un modelo requiere mucha más memoria que la inferencia del modelo.
Cuando se ejecuta un modelo en inferencia, la memoria requerida es más o menos la memoria que se necesita para calcular el único tensor más grande en el modelo. Por otro lado, al entrenar un modelo, la memoria requerida es más o menos la suma de todos los tensores diferenciables.
Esto no es sorprendente si consideramos cómo funciona la auto diferenciación en los marcos de aprendizaje profundo. Estas diapositivas de conferencias de Roger Grosse de la Universidad de Toronto son excelentes para comprender mejor la auto diferenciación.
En pocas palabras, para calcular el gradiente de una función diferenciable (por ejemplo, una capa), la auto diferenciación requiere el gradiente de la salida de la función y el tensor de entrada y salida de la función. Si bien los gradientes se calculan de forma dinámica y luego se descartan, los tensores de entrada y salida (también conocidos como activaciones) de una función se almacenan durante el paso hacia adelante.
Bien, apliquemos esto a un modelo transformador. Un modelo transformador incluye una pila de múltiples capas de transformador. Cada capa de transformador adicional obliga al modelo a almacenar más activaciones durante el paso hacia adelante y, por lo tanto, aumenta la memoria requerida para el entrenamiento. Echemos un vistazo más detallado. Una capa de transformador consiste esencialmente en dos capas residuales. La primera capa residual representa el mecanismo de autoatención como se explica en la sección 1) y la segunda capa residual representa las capas lineales o de alimentación hacia adelante como se explica en la sección 2).
Usando la misma notación que antes, la entrada de una capa de transformador, es decir, X \mathbf{X} X, se normaliza primero 1 ^{1} 1 y luego se procesa mediante la capa de autoatención para obtener la salida Z = SelfAttn ( LayerNorm ( X ) ) \mathbf{Z} = \text{SelfAttn}(\text{LayerNorm}(\mathbf{X})) Z = SelfAttn ( LayerNorm ( X ) ) . Abreviaremos estas dos capas con G G G para que Z = G ( X ) \mathbf{Z} = G(\mathbf{X}) Z = G ( X ) . A continuación, se agrega la residual Z \mathbf{Z} Z a la entrada Z ‾ = Z + X \mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X} Z = Z + X y la suma se alimenta en la segunda capa residual, es decir, las dos capas lineales. Z ‾ \mathbf{\overline{Z}} Z se procesa mediante una segunda capa de normalización, seguida de las dos capas lineales para obtener Y = Linear ( LayerNorm ( Z + X ) ) \mathbf{Y} = \text{Linear}(\text{LayerNorm}(\mathbf{Z} + \mathbf{X})) Y = Linear ( LayerNorm ( Z + X ) ) . Abreviaremos la segunda capa de normalización y las dos capas lineales con F F F, lo que da como resultado Y = F ( Z ‾ ) \mathbf{Y} = F(\mathbf{\overline{Z}}) Y = F ( Z ) . Finalmente, la residual Y \mathbf{Y} Y se agrega a Z ‾ \mathbf{\overline{Z}} Z para obtener la salida de la capa de transformador Y ‾ = Y + Z ‾ \mathbf{\overline{Y}} = \mathbf{Y} + \mathbf{\overline{Z}} Y = Y + Z .
Vamos a ilustrar una capa completa de transformador utilizando el ejemplo de x 1 , … , x 16 \mathbf{x}_1, \ldots, \mathbf{x}_{16} x 1 , … , x 1 6 .
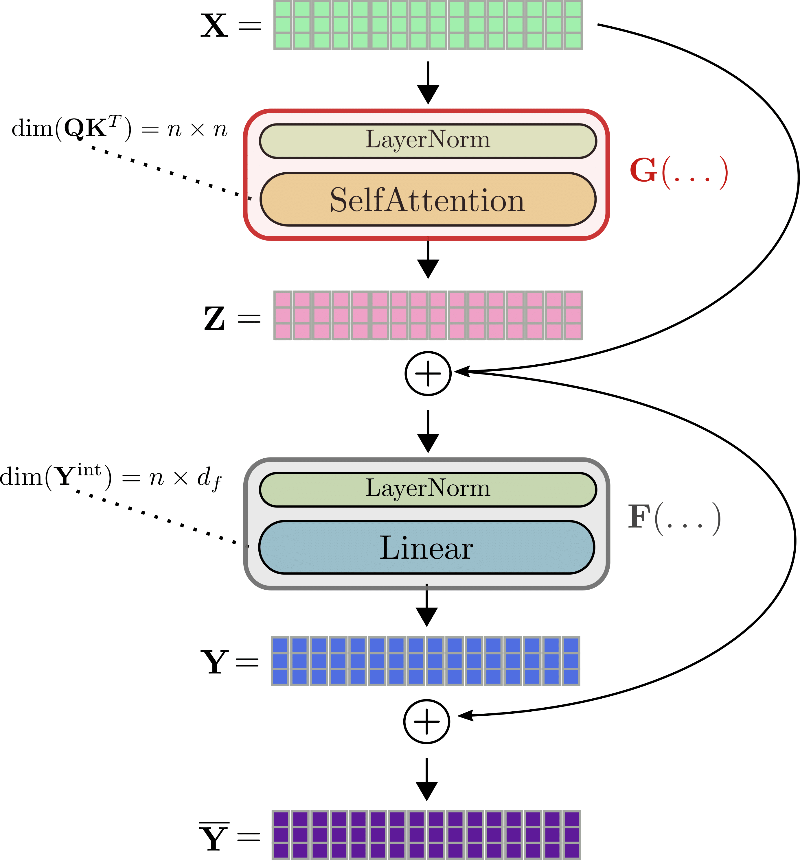
Para calcular el gradiente de, por ejemplo, el bloque de auto-atención G G G , se deben conocer de antemano tres tensores: el gradiente ∂ Z \partial \mathbf{Z} ∂ Z , la salida Z \mathbf{Z} Z y la entrada X \mathbf{X} X . Mientras que el gradiente ∂ Z \partial \mathbf{Z} ∂ Z se puede calcular sobre la marcha y descartar después, los valores de Z \mathbf{Z} Z y X \mathbf{X} X deben calcularse y almacenarse durante el paso hacia adelante, ya que no es posible recalcularlos fácilmente sobre la marcha durante la retropropagación. Por lo tanto, durante el paso hacia adelante, se deben almacenar en memoria grandes salidas de tensores, como la matriz de producto punto consulta-clave Q K T \mathbf{Q}\mathbf{K}^T Q K T o la salida intermedia de las capas lineales Y int \mathbf{Y}^{\text{int}} Y int .
Aquí es donde entran en ayuda las capas residuales reversibles. La idea es relativamente sencilla. El bloque residual está diseñado de tal manera que, en lugar de tener que almacenar el tensor de entrada y salida de una función, ambos se pueden recalcular fácilmente durante el paso hacia atrás, de modo que no se tenga que almacenar ningún tensor en memoria durante el paso hacia adelante. Esto se logra utilizando dos flujos de entrada X ( 1 ) , X ( 2 ) \mathbf{X}^{(1)}, \mathbf{X}^{(2)} X ( 1 ) , X ( 2 ) y dos flujos de salida Y ‾ ( 1 ) , Y ‾ ( 2 ) \mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)} Y ( 1 ) , Y ( 2 ) . El primer residual Z \mathbf{Z} Z se calcula mediante el primer flujo de salida Z = G ( X ( 1 ) ) \mathbf{Z} = G(\mathbf{X}^{(1)}) Z = G ( X ( 1 ) ) y se agrega posteriormente a la entrada del segundo flujo de entrada, de modo que Z ‾ = Z + X ( 2 ) \mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}^{(2)} Z = Z + X ( 2 ) . De manera similar, el residual Y = F ( Z ‾ ) \mathbf{Y} = F(\mathbf{\overline{Z}}) Y = F ( Z ) se agrega al primer flujo de entrada nuevamente, de modo que los dos flujos de salida se definen mediante Y ( 1 ) = Y + X ( 1 ) \mathbf{Y}^{(1)} = \mathbf{Y} + \mathbf{X}^{(1)} Y ( 1 ) = Y + X ( 1 ) y Y ( 2 ) = X ( 2 ) + Z = Z ‾ \mathbf{Y}^{(2)} = \mathbf{X}^{(2)} + \mathbf{Z} = \mathbf{\overline{Z}} Y ( 2 ) = X ( 2 ) + Z = Z .
La capa reversible del transformador se puede visualizar para x 1 , … , x 16 \mathbf{x}_1, \ldots, \mathbf{x}_{16} x 1 , … , x 1 6 de la siguiente manera.
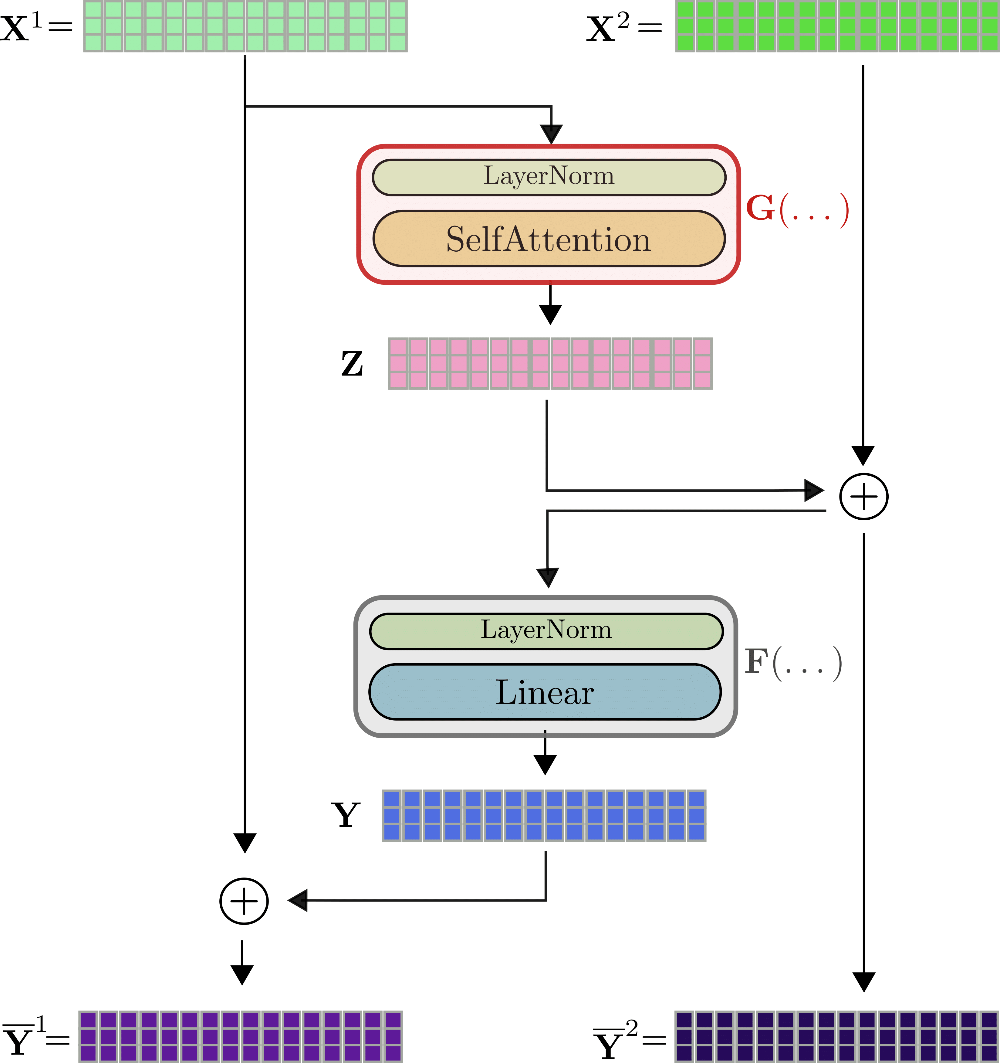
Como se puede ver, las salidas Y ‾ ( 1 ) , Y ‾ ( 2 ) \mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)} Y ( 1 ) , Y ( 2 ) se calculan de manera muy similar a Y ‾ \mathbf{\overline{Y}} Y de la capa no reversible, pero son matemáticamente diferentes. Los autores de Reformer observan en algunos experimentos iniciales que el rendimiento de un modelo de transformador reversible coincide con el rendimiento de un modelo de transformador estándar. La primera diferencia visible con respecto a la capa de transformador estándar es que hay dos flujos de entrada y dos flujos de salida 3 ^{3} 3 , lo que al principio aumenta ligeramente la memoria requerida para ambos el paso hacia adelante. La arquitectura de dos flujos es crucial, sin embargo, para no tener que guardar ninguna activación durante el paso hacia adelante. Explicaremos esto. Para la retropropagación, la capa reversible del transformador debe calcular los gradientes ∂ G \partial G ∂ G y ∂ F \partial F ∂ F . Además de los gradientes ∂ Y \partial \mathbf{Y} ∂ Y y ∂ Z \partial \mathbf{Z} ∂ Z que se pueden calcular sobre la marcha, se deben conocer los valores del tensor Y \mathbf{Y} Y , Z ‾ \mathbf{\overline{Z}} Z para ∂ F \partial F ∂ F y los valores del tensor Z \mathbf{Z} Z y X ( 1 ) \mathbf{X}^{(1)} X ( 1 ) para ∂ G \partial G ∂ G para que funcione la auto-diferenciación.
Si asumimos que conocemos Y ‾ ( 1 ) , Y ‾ ( 2 ) \mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)} Y ( 1 ) , Y ( 2 ) , es fácil representar en el gráfico que se puede calcular X ( 1 ) , X ( 2 ) \mathbf{X}^{(1)}, \mathbf{X}^{(2)} X ( 1 ) , X ( 2 ) de la siguiente manera. X ( 1 ) = F ( Y ‾ ( 1 ) ) − Y ‾ ( 1 ) \mathbf{X}^{(1)} = F(\mathbf{\overline{Y}}^{(1)}) – \mathbf{\overline{Y}}^{(1)} X ( 1 ) = F ( Y ( 1 ) ) − Y ( 1 ) . Genial, ahora que X ( 1 ) \mathbf{X}^{(1)} X ( 1 ) se conoce, X ( 2 ) \mathbf{X}^{(2)} X ( 2 ) se puede calcular mediante X ( 2 ) = Y ‾ ( 1 ) − G ( X ( 1 ) ) \mathbf{X}^{(2)} = \mathbf{\overline{Y}}^{(1)} – G(\mathbf{X}^{(1)}) X ( 2 ) = Y ( 1 ) − G ( X ( 1 ) ) . Ahora bien, Z \mathbf{Z} Z e Y \mathbf{Y} Y son fáciles de calcular mediante Y = Y ‾ ( 1 ) − X ( 1 ) \mathbf{Y} = \mathbf{\overline{Y}}^{(1)} – \mathbf{X}^{(1)} Y = Y ( 1 ) − X ( 1 ) y Z = Y ‾ ( 2 ) − X ( 2 ) \mathbf{Z} = \mathbf{\overline{Y}}^{(2)} – \mathbf{X}^{(2)} Z = Y ( 2 ) − X ( 2 ) . Entonces, en conclusión, si solo se almacenan las salidas Y ‾ ( 1 ) , Y ‾ ( 2 ) \mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)} Y ( 1 ) , Y ( 2 ) de la última capa reversible del transformador durante el pase hacia adelante, todas las demás activaciones relevantes se pueden derivar utilizando G G G y F F F durante el pase hacia atrás y pasando X ( 1 ) \mathbf{X}^{(1)} X ( 1 ) y X ( 2 ) \mathbf{X}^{(2)} X ( 2 ) . El costo adicional de dos pases hacia adelante de G G G y F F F por capa reversible del transformador durante la retropropagación se intercambia por no tener que almacenar ninguna activación durante el pase hacia adelante. ¡No está mal!
Nota: Recientemente, los principales frameworks de aprendizaje profundo han lanzado código que permite almacenar solo ciertas activaciones y volver a calcular las más grandes durante la propagación hacia atrás (TensorFlow aquí y PyTorch aquí). Para capas reversibles estándar, esto aún significa que al menos una activación debe ser almacenada para cada capa del transformador, pero al definir qué activaciones se pueden volver a calcular dinámicamente, se puede ahorrar mucha memoria.
1 ^{1} 1 En las dos secciones anteriores, hemos omitido las capas de normalización de capa que preceden tanto la capa de autoatención como las capas lineales. El lector debe saber que tanto X \mathbf{X} X como Z ‾ \mathbf{\overline{Z}} Z son procesados por normalización de capa antes de ser alimentados en la autoatención y las capas lineales respectivamente. 2 ^{2} 2 Mientras que en el diseño la dimensión de Q K \mathbf{Q}\mathbf{K} Q K se escribe como n × n n \times n n × n , en una capa de autoatención LSH o autoatención local, la dimensión sería solo n × l c × n h n \times l_{c} \times n_{h} n × l c × n h o n × l c n \times l_{c} n × l c respectivamente, donde l c l_{c} l c es la longitud de fragmento y n h n_{h} n h es el número de hashes 3 ^{3} 3 En la primera capa reversible del transformador, X ( 2 ) \mathbf{X}^{(2)} X ( 2 ) se establece como igual a X ( 1 ) \mathbf{X}^{(1)} X ( 1 ) .
Benchmark
Para medir el efecto de las capas residuales reversibles, compararemos el consumo de memoria de BERT con Reformer durante el entrenamiento para un número creciente de capas.
#@title Instalaciones e importaciones
# Instalaciones con pip
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, BertConfig, PyTorchBenchmark, PyTorchBenchmarkArgumentsVamos a medir la memoria requerida para el modelo estándar bert-base-uncased de BERT aumentando el número de capas de 4 a 12.
config_4_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=4)
config_8_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=8)
config_12_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=12)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Bert-4-Layers", "Bert-8-Layers", "Bert-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_bert, config_8_layers_bert, config_12_layers_bert], args=benchmark_args)
result = benchmark.run()
HBox(children=(FloatProgress(value=0.0, description='Descargando', max=433.0, style=ProgressStyle(description_…
1 / 3
2 / 3
3 / 3
==================== ENTRENAMIENTO - MEMORIA - RESULTADOS ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Batch Longitud de la Secuencia Memoria en MB
--------------------------------------------------------------------------------
Bert-4-Layers 8 512 4103
Bert-8-Layers 8 512 5759
Bert-12-Layers 8 512 7415
--------------------------------------------------------------------------------Se puede observar que añadir una sola capa de BERT aumenta linealmente la memoria requerida en más de 400MB.
config_4_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=4, num_hashes=1)
config_8_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=8, num_hashes=1)
config_12_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=12, num_hashes=1)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-4-Layers", "Reformer-8-Layers", "Reformer-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_reformer, config_8_layers_reformer, config_12_layers_reformer], args=benchmark_args)
result = benchmark.run()
1 / 3
2 / 3
3 / 3
==================== ENTRENAMIENTO - MEMORIA - RESULTADOS ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Batch Longitud de la Secuencia Memoria en MB
--------------------------------------------------------------------------------
Reformer-4-Layers 8 512 4607
Reformer-8-Layers 8 512 4987
Reformer-12-Layers 8 512 5367
--------------------------------------------------------------------------------En cambio, para Reformer, añadir una capa añade significativamente menos memoria en la práctica. Añadir una sola capa aumenta la memoria requerida en promedio en menos de 100MB, de modo que un modelo de 12 capas reformer-enwik8 mucho más grande requiere menos memoria que un modelo de 12 capas bert-base-uncased.
4. Codificaciones posicionales axiales
Reformer hace posible procesar secuencias de entrada enormes. Sin embargo, para secuencias de entrada tan largas, las matrices de pesos de codificación posicional estándar solas usarían más de 1GB para almacenar sus pesos. Para evitar tales matrices de codificación posicional grandes, el código oficial de Reformer introdujo las Codificaciones Posicionales Axiales.
Importante: Las Codificaciones Posicionales Axiales no se explicaron en el artículo oficial, pero se pueden entender bien al examinar el código y hablar con los autores
Codificación Posicional Axial en Reformer
Los Transformers necesitan codificaciones posicionales para tener en cuenta el orden de las palabras en la entrada, ya que las capas de auto-atención no tienen noción del orden. Las codificaciones posicionales suelen definirse mediante una matriz de búsqueda simple E = [ e 1 , … , e n max ] \mathbf{E} = \left[\mathbf{e}_1, \ldots, \mathbf{e}_{n_\text{max}}\right] E = [ e 1 , … , e n max ] El vector de codificación posicional e i \mathbf{e}_{i} e i se suma simplemente al vector de entrada i-ésimo x i + e i \mathbf{x}_{i} + \mathbf{e}_{i} x i + e i para que el modelo pueda distinguir si un vector de entrada (también conocido como token) está en la posición i i i o j j j . Para cada posición de entrada, el modelo necesita poder buscar el vector de codificación posicional correspondiente, de modo que la dimensión de E \mathbf{E} E está definida por la longitud máxima de los vectores de entrada que el modelo puede procesar config.max_position_embeddings, es decir, n max n_\text{max} n max , y el config.hidden_size, es decir, d h d_{h} d h de los vectores de entrada.
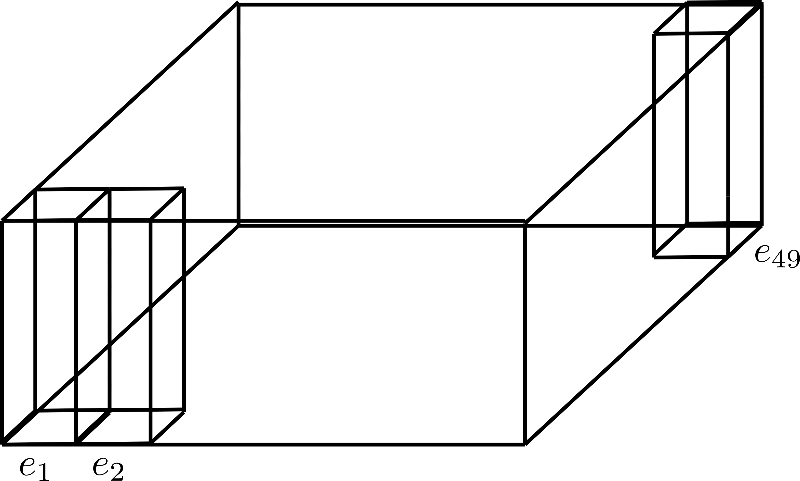
Suponiendo d h = 4 d_{h}=4 d h = 4 y n max = 49 n_\text{max}=49 n max = 4 9 , una matriz de codificación posicional de este tipo se puede visualizar de la siguiente manera:

Aquí, mostramos solo las codificaciones posicionales e 1 \mathbf{e}_{1} e 1 , e 2 \mathbf{e}_{2} e 2 y e 49 \mathbf{e}_{49} e 4 9 cada una de dimensión, también conocida como altura 4.
Imaginemos que queremos entrenar un modelo Reformer en secuencias de hasta 0.5M tokens y un vector de entrada config.hidden_size de 1024 (ver cuaderno aquí ). Las incrustaciones posicionales correspondientes tienen un tamaño de 0.5 M × 1024 ∼ 512 M 0.5M \times 1024 \sim 512M 0 . 5 M × 1 0 2 4 ∼ 5 1 2 M parámetros, lo que corresponde a un tamaño de 2GB.
Estas codificaciones posicionales usarían una cantidad innecesariamente grande de memoria tanto al cargar el modelo en la memoria como al guardar el modelo en un disco duro.
Los autores de Reformer lograron reducir drásticamente el tamaño de las codificaciones posicionales al reducir a la mitad la dimensión config.hidden_size y factorizar de manera inteligente la dimensión n max n_\text{max} n max . En Transformer, el usuario puede decidir en qué forma se puede factorizar n max n_\text{max} n max estableciendo config.axial_pos_shape en una lista adecuada de dos valores n max 1 n_\text{max}^1 n max 1 y n max 2 n_\text{max}^2 n max 2 para que n max 1 × n max 2 = n max n_\text{max}^1 \times n_\text{max}^2 = n_\text{max} n max 1 × n max 2 = n max . Al establecer config.axial_pos_embds_dim en una lista adecuada de dos valores d h 1 d_{h}^{1} d h 1 y d h 2 d_{h}^2 d h 2 para que d h 1 + d h 2 = d h d_{h}^1 + d_{h}^2 = d_{h} d h 1 + d h 2 = d h , el usuario puede decidir cómo se debe dividir la dimensión del tamaño oculto. Ahora, visualicemos y expliquemos de manera más intuitiva.
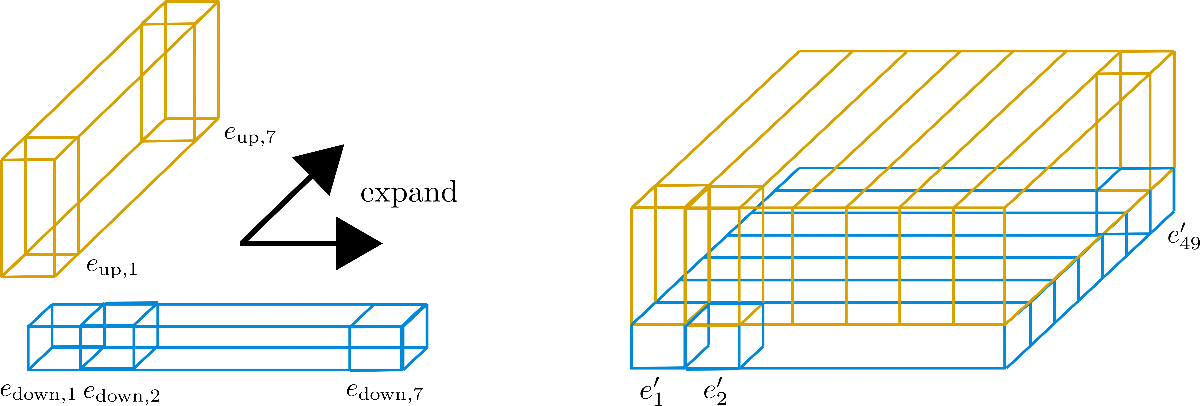
Se puede pensar en factorizar n max n_{\text{max}} n max como plegar la dimensión en un tercer eje, que se muestra a continuación para la factorización config.axial_pos_shape = [7, 7]:
Cada uno de los tres prismas rectangulares representa uno de los vectores de codificación e 1 , e 2 , e 49 \mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{49} e 1 , e 2 , e 4 9 , pero podemos ver que los 49 vectores de codificación se dividen en 7 filas de 7 vectores cada una. Ahora la idea es utilizar solo una fila de 7 vectores de codificación y expandir esos vectores a las otras 6 filas, reutilizando sus valores. Debido a que se desaconseja tener los mismos valores para diferentes vectores de codificación, cada vector de dimensión (también conocida como altura) config.hidden_size=4 se divide en el vector de codificación inferior e down \mathbf{e}_\text{down} e down de tamaño 1 1 1 y el vector de codificación superior e up \mathbf{e}_\text{up} e up de tamaño 3 3 3 , de modo que la parte inferior se pueda expandir a lo largo de la dimensión de fila y la parte superior se pueda expandir a lo largo de la dimensión de columna. Veámoslo visualmente para mayor claridad.
Podemos ver que hemos dividido los vectores de incrustación en e down \mathbf{e}_\text{down} e down (en azul) y e up \mathbf{e}_\text{up} e up (en amarillo). Ahora, para los “sub”-vectores E down = [ e down , 1 , … , e down , 49 ] \mathbf{E}_\text{down} = \left[\mathbf{e}_{\text{down},1}, \ldots, \mathbf{e}_{\text{down},49}\right] E down = [ e down , 1 , … , e down , 4 9 ] solo se conserva la primera fila, es decir, el ancho en el gráfico, de 7 7 7 y se expande a lo largo de la dimensión de columna, es decir, la profundidad del gráfico. Inversamente, para los “sub”-vectores E up = [ e up , 1 , … , e up , 49 ] \mathbf{E}_\text{up} = \left[\mathbf{e}_{\text{up},1}, \ldots, \mathbf{e}_{\text{up},49}\right] E up = [ e up , 1 , … , e up , 4 9 ] solo se conserva la primera columna de 7 7 7 y se expande a lo largo de la dimensión de fila. Los nuevos vectores de incrustación resultantes e ′ i \mathbf{e’}_{i} e ′ i corresponden a
e ′ i = [ [ e down, i % n max 1 ] T , [ e up, ⌊ i n max 2 ⌋ ] T ] T \mathbf{e’}_{i} = \left[ \left[\mathbf{e}_{\text{down, } i \% n_\text{max}^1}\right]^T, \left[\mathbf{e}_{\text{up, } \left \lfloor{\frac{i}{{n}^2_{\text{max}}}}\right \rfloor} \right]^T \right]^T e ′ i = ⎣ ⎢ ⎢ ⎡ [ e down, i % n max 1 ] T , ⎣ ⎢ ⎡ e up, ⌊ n max 2 i ⌋ ⎦ ⎥ ⎤ T ⎦ ⎥ ⎥ ⎤ T
mientras que n max 1 = 7 n_\text{max}^1 = 7 n max 1 = 7 y n max 2 = 7 n_\text{max}^2 = 7 n max 2 = 7 en nuestro ejemplo. Estas nuevas codificaciones E ′ = [ e ′ 1 , … , e ′ n max ] \mathbf{E’} = \left[\mathbf{e’}_{1}, \ldots, \mathbf{e’}_{n_\text{max}}\right] E ′ = [ e ′ 1 , … , e ′ n max ] se llaman Codificaciones de Posición Axiales.
En lo siguiente, se ilustran con más detalle estas codificaciones de posición axial para nuestro ejemplo.
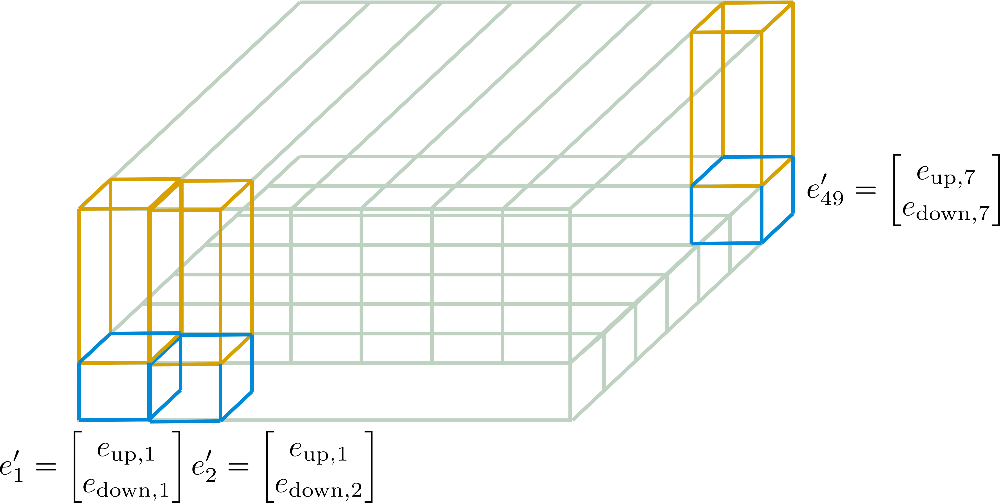
Ahora debería ser más comprensible cómo se calculan los vectores de codificación posicional final E ′ \mathbf{E’} E ′ solo a partir de E down \mathbf{E}_{\text{down}} E down de dimensión d h 1 × n max 1 d_{h}^1 \times n_{\text{max}^1} d h 1 × n max 1 y E up \mathbf{E}_{\text{up}} E up de dimensión d h 2 × n max 2 d_{h}^2 \times n_{\text{max}}^2 d h 2 × n max 2 .
El aspecto crucial a tener en cuenta aquí es que las Codificaciones Posicionales Axiales se aseguran de que ninguno de los vectores [ e ′ 1 , … , e ′ n max ] \left[\mathbf{e’}_1, \ldots, \mathbf{e’}_{n_{\text{max}}}\right] [ e ′ 1 , … , e ′ n max ] sean iguales entre sí por diseño y que el tamaño general de la matriz de codificación se reduzca de n max × d h n_{\text{max}} \times d_{h} n max × d h a n max 1 × d h 1 + n max 2 × d h 2 n_{\text{max}}^1 \times d_{h}^1 + n_\text{max}^2 \times d_{h}^2 n max 1 × d h 1 + n max 2 × d h 2 . Al permitir que cada vector de codificación posicional axial sea diferente por diseño, el modelo tiene mucha más flexibilidad para aprender representaciones posicionales eficientes si las codificaciones posicionales axiales son aprendidas por el modelo.
Para demostrar la drástica reducción en tamaño, supongamos que hubiéramos establecido config.axial_pos_shape = [1024, 512] y config.axial_pos_embds_dim = [512, 512] para un modelo Reformer que pueda procesar entradas de hasta 0.5M tokens. La matriz de codificación posicional axial resultante habría tenido un tamaño de solo 1024 × 512 + 512 × 512 ∼ 800 K 1024 \times 512 + 512 \times 512 \sim 800K 1 0 2 4 × 5 1 2 + 5 1 2 × 5 1 2 ∼ 8 0 0 K parámetros, lo que corresponde aproximadamente a 3MB. Esta es una reducción drástica en comparación con los 2GB que requeriría una matriz de codificación posicional estándar en este caso.
Para una explicación más condensada y matemáticamente más pesada, consulte la documentación de 🤗Transformers aquí .
Benchmarks
Por último, también comparemos el consumo máximo de memoria de las codificaciones posicionales convencionales con las codificaciones posicionales axiales .
#@title Instalaciones e Importaciones
# Instalaciones de pip
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments, ReformerModelLas codificaciones posicionales dependen solo de dos parámetros de configuración: la longitud máxima permitida de las secuencias de entrada config.max_position_embeddings y config.hidden_size . Usemos un modelo que empuje la longitud máxima permitida de las secuencias de entrada a medio millón de tokens, llamado google/reformer-crime-and-punishment , para ver el efecto de usar codificaciones posicionales axiales.
Para empezar, compararemos la forma de las codificaciones de posición axial con las codificaciones posicionales estándar y el número de parámetros en el modelo.
config_no_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=False) # desactivar codificaciones posicionales axiales
config_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=True, axial_pos_embds_dim=(64, 192), axial_pos_shape=(512, 1024)) # habilitar codificaciones posicionales axiales
print("Codificaciones posicionales predeterminadas")
print(20 * '-')
model = ReformerModel(config_no_pos_axial_embeds)
print(f"Forma de las codificaciones posicionales: {model.embeddings.position_embeddings}")
print(f"Número de parámetros del modelo: {model.num_parameters()}")
print(20 * '-' + '\n\n')
print("Codificaciones posicionales axiales")
print(20 * '-')
model = ReformerModel(config_pos_axial_embeds)
print(f"Forma de las codificaciones posicionales: {model.embeddings.position_embeddings}")
print(f"Número de parámetros del modelo: {model.num_parameters()}")
print(20 * '-' + '\n\n')
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1151.0, style=ProgressStyle(description…
Codificaciones posicionales predeterminadas
--------------------
Forma de las codificaciones posicionales: PositionEmbeddings(
(embedding): Embedding(524288, 256)
)
Número de parámetros del modelo: 136572416
--------------------
Codificaciones posicionales axiales
--------------------
Forma de las codificaciones posicionales: AxialPositionEmbeddings(
(weights): ParameterList(
(0): Parameter containing: [torch.FloatTensor of size 512x1x64]
(1): Parameter containing: [torch.FloatTensor of size 1x1024x192]
)
)
Número de parámetros del modelo: 2584064
--------------------Habiendo leído la teoría, la forma de los pesos de codificación posicional axial no debería sorprender al lector.
En cuanto a los resultados, se puede observar que para modelos capaces de procesar secuencias de entrada tan largas, no es práctico utilizar codificaciones posicionales predeterminadas. En el caso de google/reformer-crime-and-punishment, las codificaciones posicionales estándar por sí solas contienen más de 100M de parámetros. Las codificaciones posicionales axiales reducen este número a poco más de 200K.
Por último, también comparemos la memoria requerida en el momento de la inferencia.
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-No-Axial-Pos-Embeddings", "Reformer-Axial-Pos-Embeddings"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_pos_axial_embeds, config_pos_axial_embeds], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== INFERENCE - MEMORY - RESULT ====================
--------------------------------------------------------------------------------
Nombre del Modelo Tamaño del Lote Longitud de Seq Memoria en MB
--------------------------------------------------------------------------------
Reformer-No-Axial-Pos-Embeddin 8 512 959
Reformer-Axial-Pos-Embeddings 8 512 447
--------------------------------------------------------------------------------Se puede observar que el uso de incrustaciones posicionales axiales reduce los requisitos de memoria aproximadamente a la mitad en el caso de google/reformer-crime-and-punishment.
We will continue to update Zepes; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
- Cómo aceleramos la inferencia del transformador 100 veces para los clientes de la API de 🤗
- Ajusta más y entrena más rápido con ZeRO a través de DeepSpeed y FairScale
- Recuperación Mejorada de Generación con Huggingface Transformers y Ray
- Hugging Face Reads, Feb. 2021 – Transformers de largo alcance
- Comprendiendo la Atención Esparsa por Bloques de BigBird
- Entrenamiento distribuido Entrena BART/T5 para resumir utilizando 🤗 Transformers y Amazon SageMaker
- Escalando la inferencia de BERT en CPU (Parte 1)






