Dominando Monte Carlo Cómo simular tu camino hacia mejores modelos de aprendizaje automático

Dominando Monte Carlo Simulando para mejorar modelos de aprendizaje automático

Aplicación de Enfoques Probabilísticos Mejorando los Algoritmos Predictivos a través de Técnicas de Simulación

Cómo un Científico Jugando a las Cartas Cambió para Siempre el Juego de la Estadística

En el tumultuoso año de 1945, mientras el mundo estaba dominado por los últimos estertores de la Segunda Guerra Mundial, un juego de solitario desató discretamente un avance en el ámbito de la computación. No era un juego ordinario, sino uno que llevaría al nacimiento del método de Monte Carlo(1). ¿El jugador? Nada menos que el científico Stanislaw Ulam, quien también estaba profundamente absorto en el Proyecto Manhattan(2). Ulam, convaleciente de una enfermedad, se vio envuelto en el solitario. Las complejas probabilidades del juego lo intrigaron, y se dio cuenta de que simular repetidamente el juego podría proporcionar una buena aproximación de estas probabilidades(3). Fue un momento de iluminación, similar a la manzana de Newton, pero con cartas en lugar de fruta. Ulam luego discutió estas ideas con su colega John von Neumann, y juntos formalizaron el método de Monte Carlo, nombrado en honor al famoso Casino de Monte Carlo en Mónaco (representado en la famosa pintura de Edvard Munch que se muestra arriba), donde las apuestas son altas y la suerte reina, al igual que el método en sí mismo.

Avanzamos rápidamente hasta los días presentes, y el método de Monte Carlo se ha convertido en un as bajo la manga en el mundo del aprendizaje automático, incluyendo aplicaciones en el aprendizaje por refuerzo, el filtrado bayesiano y la optimización de modelos intricados(4). Su robustez y versatilidad han asegurado su relevancia continua, más de siete décadas después de su concepción. Desde los juegos de solitario de Ulam hasta las sofisticadas aplicaciones de IA de hoy en día, el método de Monte Carlo sigue siendo un testimonio del poder de la simulación y la aproximación para abordar sistemas complejos.

Jugando tus Cartas Correctamente con Simulaciones Probabilísticas

En el intrincado mundo de la ciencia de datos y el aprendizaje automático, las simulaciones de Monte Carlo son como una apuesta bien calculada. Esta técnica estadística nos permite hacer apuestas estratégicas frente a la incertidumbre, dando sentido probabilístico a problemas complejos y deterministas. En este artículo, desmitificaremos las simulaciones de Monte Carlo y exploraremos sus poderosas aplicaciones en estadísticas y aprendizaje automático.

Comenzaremos sumergiéndonos en la teoría detrás de las simulaciones de Monte Carlo, iluminando los principios que hacen de esta técnica una herramienta poderosa para la resolución de problemas. Trabajaremos en algunas aplicaciones prácticas en Python, demostrando cómo se pueden implementar las simulaciones de Monte Carlo en la práctica.

• Registro KYC ahora hecho fácil usando IA
• Stability AI ha lanzado Beluga 1 y Stable Beluga 2, nuevos LLM de acceso abierto.
• Automatiza la creación de subtítulos y la búsqueda de imágenes a escala empresarial utilizando la inteligencia artificial generativa y Amazon Kendra

Luego, exploraremos cómo se pueden utilizar las simulaciones de Monte Carlo para optimizar modelos de aprendizaje automático. Nos enfocaremos en la tarea a menudo desafiante de la sintonización de hiperparámetros, brindando un conjunto de herramientas prácticas para navegar este paisaje complejo.

Así que, haz tus apuestas y ¡comencemos!

Comprendiendo las Simulaciones de Monte Carlo

Las simulaciones de Monte Carlo son una técnica invaluable para matemáticos y científicos de datos. Estas simulaciones proporcionan una metodología para navegar a través de una amplia y compleja variedad de posibilidades, formulando suposiciones educadas y refinando progresivamente las opciones hasta que la solución más adecuada emerja.

La forma en que funciona es así: generamos una gran cantidad de escenarios aleatorios, siguiendo un cierto proceso predefinido, y luego examinamos estos escenarios para estimar la probabilidad de diversos resultados. Aquí tienes una analogía para hacerlo más claro: considera cada escenario como un turno en el popular juego de mesa de Hasbro “Clue”. Para aquellos no familiarizados, “Clue” es un juego de estilo detectivesco en el que los jugadores se mueven por una mansión, recopilando pruebas para deducir los detalles de un crimen: quién, qué y dónde. Cada turno, o pregunta formulada, elimina respuestas potenciales y acerca a los jugadores a revelar el verdadero escenario del crimen. De manera similar, cada simulación en un estudio de Monte Carlo proporciona información que nos acerca a la solución de nuestro problema complejo.

En el ámbito del aprendizaje automático, estos “escenarios” pueden representar diferentes configuraciones de modelos, conjuntos variados de hiperparámetros, formas alternativas de dividir un conjunto de datos en conjuntos de entrenamiento y prueba, y muchas otras aplicaciones. Al evaluar los resultados de estos escenarios, podemos obtener conocimientos valiosos sobre el comportamiento de nuestro algoritmo de aprendizaje automático, lo que nos permite tomar decisiones informadas sobre su optimización.

Un Juego de Dardos

Para entender las simulaciones de Monte Carlo, imagina que estás jugando un juego de dardos. Pero en lugar de apuntar a un objetivo específico, estás vendado y lanzando los dardos al azar en un gran tablero de dardos cuadrado. Dentro de este cuadrado, hay un objetivo circular. Tu objetivo es estimar el valor de pi, la relación entre la circunferencia del círculo y su diámetro.

Suena imposible, ¿verdad? Pero aquí está el truco: la relación entre el área del círculo y el área del cuadrado es pi/4. Entonces, si lanzas una gran cantidad de dardos, la relación entre los dardos que caen dentro del círculo y el número total de dardos debería ser aproximadamente pi/4. ¡Multiplica esta relación por 4 y tendrás una estimación de pi!

Adivinando al Azar vs. Monte Carlo

Para ilustrar el poder de las simulaciones de Monte Carlo, comparemos con un método más simple, quizás el más simple de todos: adivinar al azar.

Cuando ejecutas el código a continuación para ambos casos (aleatorio y Monte Carlo), obtendrás un conjunto diferente de predicciones cada vez. Esto es de esperarse, porque los dardos se lanzan al azar. Esta es una característica clave de las simulaciones de Monte Carlo: son inherentemente estocásticas o aleatorias. Pero a pesar de esta aleatoriedad, pueden proporcionar estimaciones muy precisas cuando se usan correctamente. Por lo tanto, aunque tus cifras no se verán exactamente iguales que las mías, contarán la misma historia.

En el primer conjunto de visualizaciones (Figura 1a a Figura 1f), hacemos una serie de suposiciones aleatorias para el valor de pi, generando cada vez un círculo basado en el valor supuesto. Vamos a darle un “empujón” a esta “aleatoriedad” en la dirección correcta y asumir que, aunque no podemos recordar el valor exacto de pi, sabemos que es mayor que 2 y menor que 4. Como puedes ver en las figuras resultantes, el tamaño del círculo varía ampliamente dependiendo de la suposición, lo que demuestra la inexactitud de este enfoque (lo cual no debería ser una sorpresa). El círculo verde en cada figura representa el círculo unitario, el círculo “real” que estamos tratando de estimar. El círculo azul se basa en nuestra suposición aleatoria.

#Adivinando al Azar el Valor de Pi# Antes de ejecutar este código, asegúrate de tener instalados los paquetes necesarios.# Puedes instalarlos usando "pip install" en tu terminal o "conda install" si estás usando un entorno conda# Importar las bibliotecas necesariasimport randomimport plotly.graph_objects as goimport numpy as np# Número de suposiciones a realizar. Ajusta esto para hacer más suposiciones y generar gráficos subsiguientesnum_suposiciones = 6# Generar las coordenadas para el círculo unitario# Usamos np.linspace para generar números equidistantes en el rango de 0 a 2*pi.# Estos representan los ángulos en el círculo unitario.theta = np.linspace(0, 2*np.pi, 100)# Las coordenadas x e y del círculo unitario son el coseno y el seno de estos ángulos, respectivamente.circulo_unitario_x = np.cos(theta)circulo_unitario_y = np.sin(theta)# Haremos varias suposiciones para el valor de pifor i in range(num_suposiciones):    # Hacer una suposición aleatoria para pi entre 2 y 4    suposicion_pi = random.uniform(2, 4)    # Generar las coordenadas para el círculo basado en la suposición    # El radio del círculo es el valor supuesto de pi dividido por 4.    radio = suposicion_pi / 4    # Las coordenadas x e y del círculo son el radio multiplicado por el coseno y el seno de los ángulos, respectivamente.    circulo_x = radio * np.cos(theta)    circulo_y = radio * np.sin(theta)    # Crear una gráfica de dispersión del círculo    fig = go.Figure()    # Añadir el círculo a la gráfica    # Usamos una traza de dispersión con modo 'lines' para dibujar el círculo.    fig.add_trace(go.Scatter(        x = circulo_x,        y = circulo_y,        mode='lines',        line=dict(            color='blue',            width=3        ),        name='Círculo Estimado'    ))    # Añadir el círculo unitario a la gráfica    fig.add_trace(go.Scatter(        x = circulo_unitario_x,        y = circulo_unitario_y,        mode='lines',        line=dict(            color='green',            width=3        ),        name='Círculo Unitario'    ))    # Actualizar el diseño de la gráfica    # Establecemos el título para incluir el valor supuesto de pi y ajustamos el tamaño y los rangos de los ejes para mostrar correctamente los círculos.    fig.update_layout(        title=f"Fig1{chr(97 + i)}: Adivinando al Azar el Valor de Pi: {suposicion_pi}",        width=600,        height=600,        xaxis=dict(            constrain="domain",            range=[-1, 1]        ),        yaxis=dict(            scaleanchor="x",            scaleratio=1,            range=[-1, 1]        )    )    # Mostrar las gráficas    fig.show()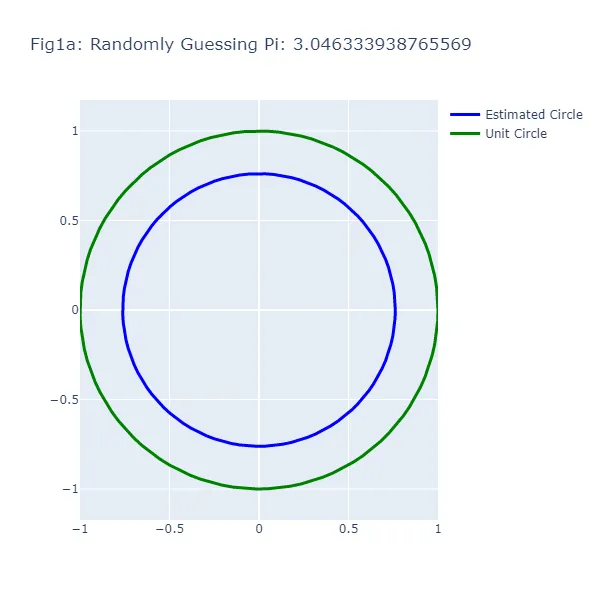

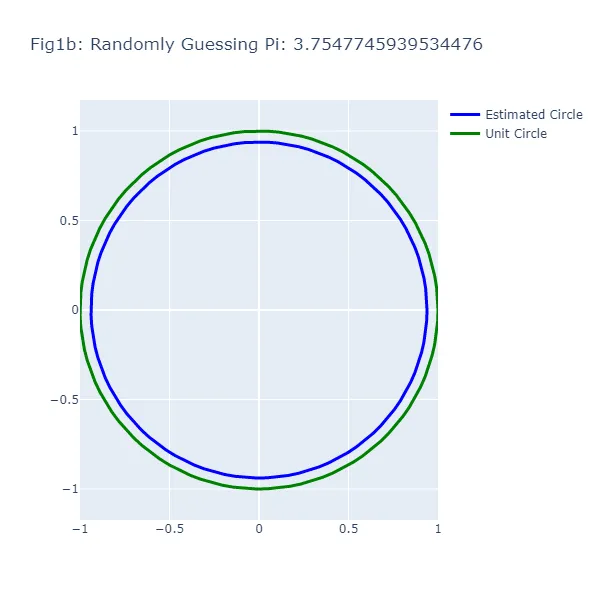
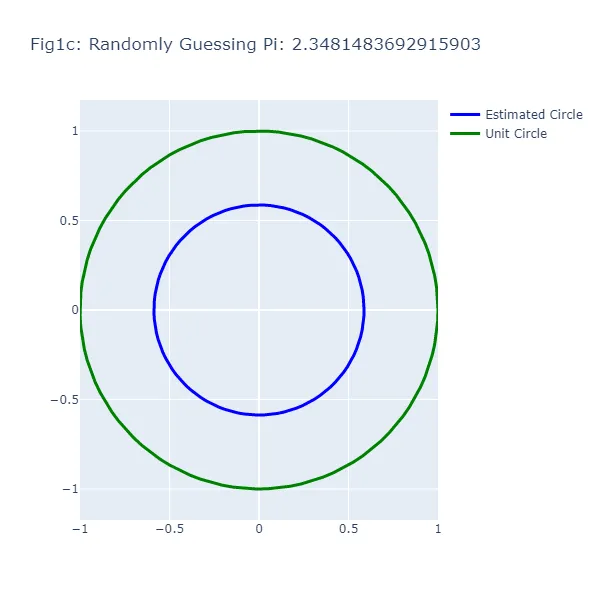
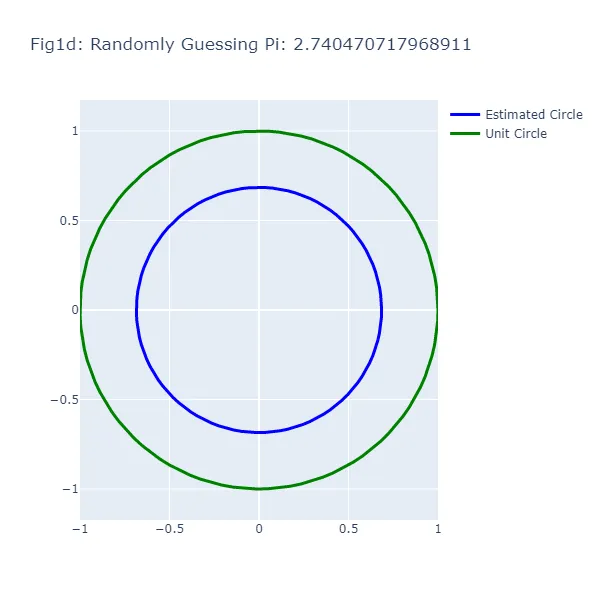
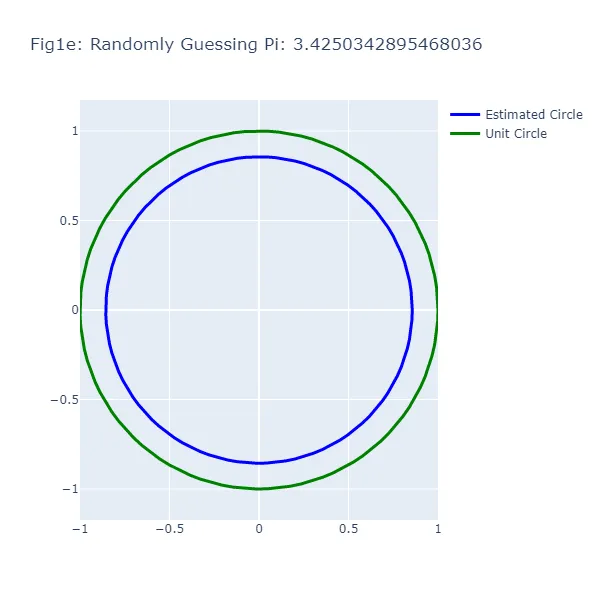
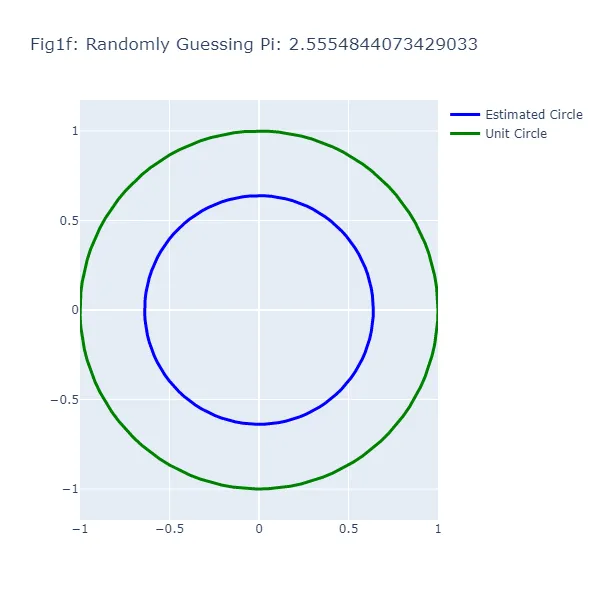
Podrás notar algo extraño: en el método de adivinanza aleatoria, a veces una suposición más cercana al valor real de pi resulta en un círculo más lejano al círculo unitario. Esta aparente contradicción surge porque estamos observando la circunferencia de los círculos, no su radio o área. La brecha visual entre los dos círculos representa el error en la estimación de la circunferencia del círculo basado en la suposición, no el círculo en su totalidad.

En el segundo conjunto de visualizaciones (Figura 2a a Figura 2f), utilizamos el método de Monte Carlo para estimar el valor de pi. En lugar de hacer una suposición aleatoria, estamos lanzando una gran cantidad de dardos a un cuadrado y contando cuántos caen dentro de un círculo inscrito en el cuadrado. La estimación resultante de pi es mucho más precisa, como se puede ver en las figuras donde el tamaño del círculo es mucho más cercano al círculo unitario real. Los puntos verdes representan los dardos que cayeron dentro del círculo unitario, y los puntos rojos representan los dardos que cayeron fuera.

#Estimación de Pi utilizando Monte Carlo# Importamos las bibliotecas necesariasimport randomimport mathimport plotly.graph_objects as goimport plotly.io as pioimport numpy as np# Simularemos lanzar dardos a un tablero para estimar pi. Lanzaremos 10,000 dardos.num_darts = 10000# Para llevar un registro de los dardos que caen en el círculo.darts_in_circle = 0# Almacenaremos las coordenadas de los dardos que caen dentro y fuera del círculo.x_coords_in, y_coords_in, x_coords_out, y_coords_out = [], [], [], []# Generaremos 6 figuras a lo largo de la simulación. Por lo tanto, crearemos una nueva figura cada 1,666 dardos (10,000 dividido por 6).num_figures = 6darts_per_figure = num_darts // num_figures# Creamos un círculo unitario para comparar nuestras estimaciones. Aquí utilizamos coordenadas polares y convertimos a coordenadas cartesianas.theta = np.linspace(0, 2*np.pi, 100)unit_circle_x = np.cos(theta)unit_circle_y = np.sin(theta)# Comenzamos a lanzar los dardos (simulando puntos aleatorios dentro de un cuadrado de 1x1 y verificando si caen dentro de un cuarto de círculo).for i in range(num_darts):    # Generamos coordenadas x, y aleatorias entre -1 y 1.    x, y = random.uniform(-1, 1), random.uniform(-1, 1)        # Si un dardo (punto) está más cerca del origen (0,0) que la distancia de 1, está dentro del círculo.    if math.sqrt(x**2 + y**2) <= 1:        darts_in_circle += 1        x_coords_in.append(x)        y_coords_in.append(y)    else:        x_coords_out.append(x)        y_coords_out.append(y)    # Después de cada 1,666 dardos, veamos cómo se ve nuestra estimación en comparación con el círculo unitario real.    if (i + 1) % darts_per_figure == 0:        # Estimamos pi viendo la proporción de dardos que cayeron en el círculo (de la cantidad total de dardos).        pi_estimate = 4 * darts_in_circle / (i + 1)        # Ahora creamos un círculo a partir de nuestra estimación para comparar visualmente con el círculo unitario.        estimated_circle_radius = pi_estimate / 4        estimated_circle_x = estimated_circle_radius * np.cos(theta)        estimated_circle_y = estimated_circle_radius * np.sin(theta)        # Graficamos los resultados usando Plotly.        fig = go.Figure()        # Agregamos los dardos que cayeron dentro y fuera del círculo a la gráfica.        fig.add_trace(go.Scattergl(x=x_coords_in, y=y_coords_in, mode='markers', name='Dardos Dentro del Círculo', marker=dict(color='green', size=4, opacity=0.8)))        fig.add_trace(go.Scattergl(x=x_coords_out, y=y_coords_out, mode='markers', name='Dardos Fuera del Círculo', marker=dict(color='red', size=4, opacity=0.8)))        # Agregamos el círculo unitario real y nuestro círculo estimado a la gráfica.        fig.add_trace(go.Scatter(x=unit_circle_x, y=unit_circle_y, mode='lines', name='Círculo Unitario', line=dict(color='green', width=3)))        fig.add_trace(go.Scatter(x=estimated_circle_x, y=estimated_circle_y, mode='lines', name='Círculo Estimado', line=dict(color='blue', width=3)))        # Personalizamos el diseño de la gráfica.        fig.update_layout(title=f"Figura {chr(97 + (i + 1) // darts_per_figure - 1)}: Dardos Lanzados: {(i + 1)}, Estimación de Pi: {pi_estimate}", width=600, height=600, xaxis=dict(constrain="domain", range=[-1, 1]), yaxis=dict(scaleanchor="x", scaleratio=1, range=[-1, 1]), legend=dict(yanchor="top", y=0.99, xanchor="left", x=0.01))        # Mostramos la gráfica.        fig.show()        # Guardamos la gráfica como un archivo de imagen PNG.        pio.write_image(fig, f"fig2{chr(97 + (i + 1) // darts_per_figure - 1)}.png")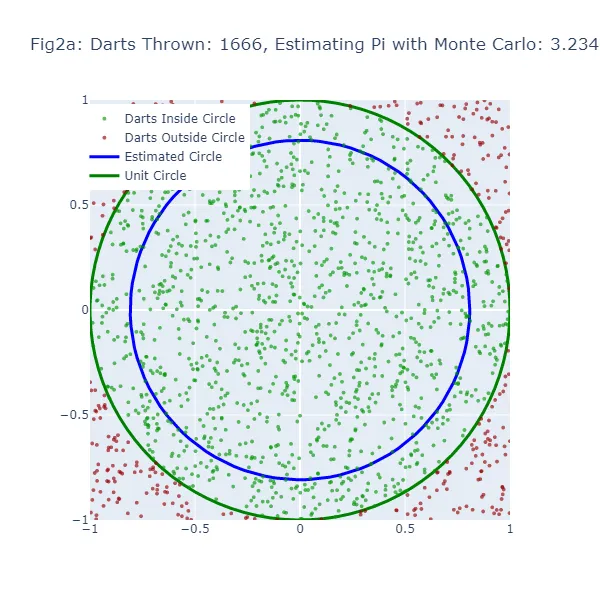

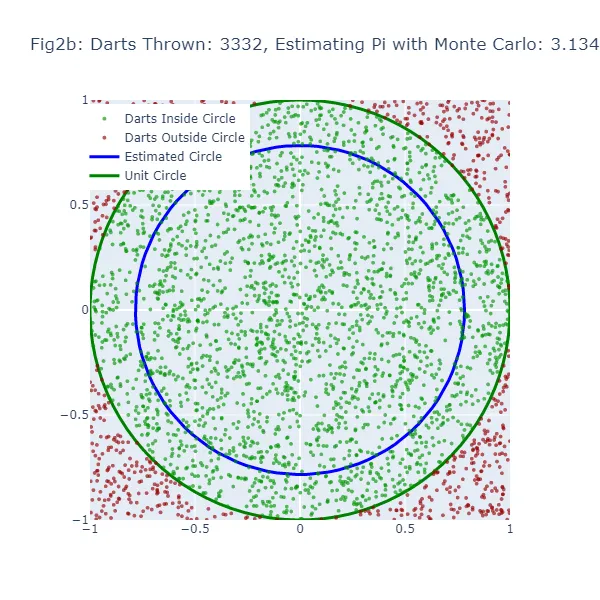
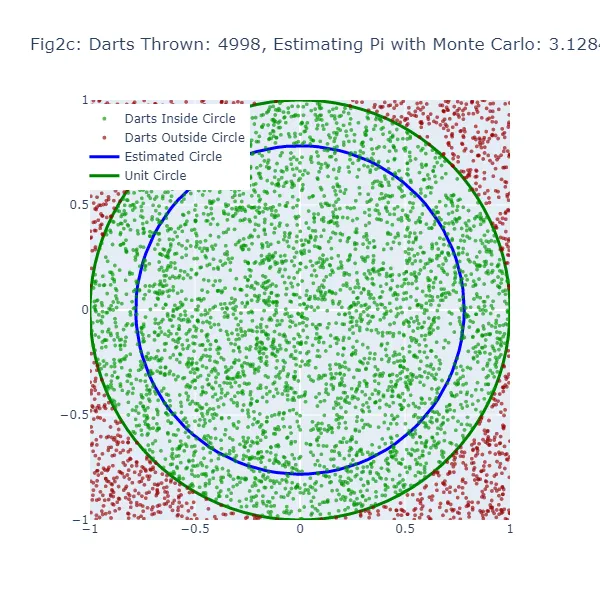
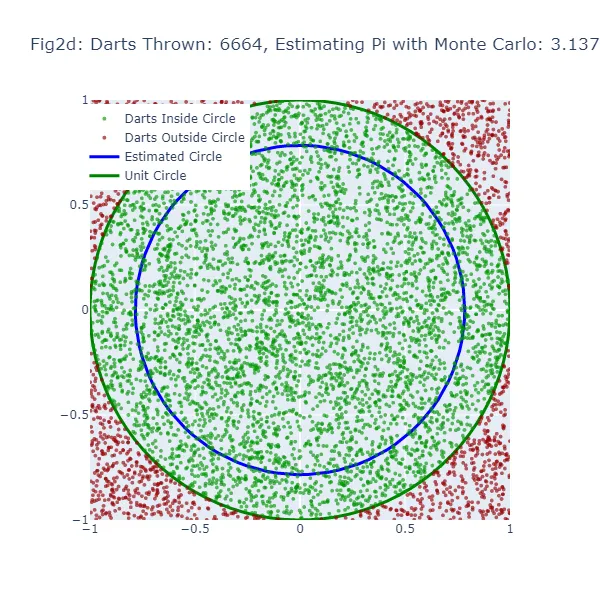
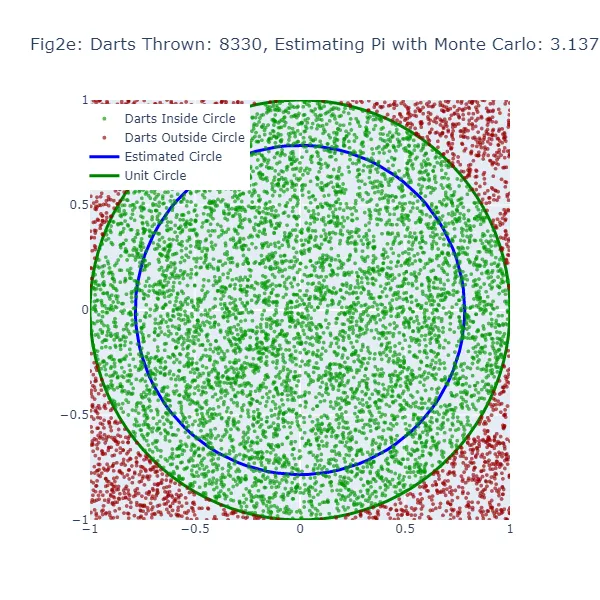
En el método de Monte Carlo, la estimación de Pi se basa en la proporción de “dardos” que caen dentro del círculo en relación con el número total de dardos lanzados. El valor estimado resultante de Pi se utiliza para generar un círculo. Si la estimación de Monte Carlo es inexacta, el círculo también tendrá un tamaño incorrecto. El ancho de la brecha entre este círculo estimado y el círculo unitario da una indicación de la precisión de la estimación de Monte Carlo.

Sin embargo, debido a que el método de Monte Carlo genera estimaciones más precisas a medida que aumenta el número de “dardos”, el círculo estimado debería converger hacia el círculo unitario a medida que se lanzan más “dardos”. Por lo tanto, aunque ambos métodos muestran una brecha cuando la estimación es inexacta, esta brecha debería disminuir de manera más consistente con el método de Monte Carlo a medida que aumenta el número de “dardos”.

Predicción de Pi: El poder de la probabilidad

Lo que hace que las simulaciones de Monte Carlo sean tan poderosas es su capacidad para aprovechar la aleatoriedad para resolver problemas deterministas. Al generar una gran cantidad de escenarios aleatorios y analizar los resultados, podemos estimar la probabilidad de diferentes resultados, incluso para problemas complejos que serían difíciles de resolver analíticamente.

En el caso de estimar pi, el método de Monte Carlo nos permite hacer una estimación muy precisa, incluso si solo estamos lanzando dardos al azar. Como se mencionó, cuantos más dardos lancemos, más precisa será nuestra estimación. Esto es una demostración de la ley de los grandes números, un concepto fundamental en la teoría de la probabilidad que establece que el promedio de los resultados obtenidos de un gran número de experimentos debe estar cerca del valor esperado, y tiende a acercarse cada vez más a medida que se realizan más experimentos. Veamos si esto tiende a ser cierto para nuestros seis ejemplos mostrados en Figuras 2a-2f trazando el número de dardos lanzados frente a la diferencia entre Pi estimado por Monte Carlo y Pi real. En general, nuestro gráfico (Figura 2g) debería mostrar una tendencia negativa. Aquí está el código para lograr esto:

# Calcular las diferencias entre Pi real y Pi estimado
diff_pi = [abs(estimate - math.pi) for estimate in pi_estimates]

# Crear la figura para el número de dardos vs diferencia en Pi (Figura 2g)
fig2g = go.Figure(data=go.Scatter(x=num_darts_thrown, y=diff_pi, mode='lines'))

# Agregar título y etiquetas al gráfico
fig2g.update_layout(
    title="Fig2g: Dardos Lanzados vs Diferencia en Pi Estimado",
    xaxis_title="Número de Dardos Lanzados",
    yaxis_title="Diferencia en Pi",
)

# Mostrar el gráfico
fig2g.show()

# Guardar el gráfico como png
pio.write_image(fig2g, "fig2g.png")

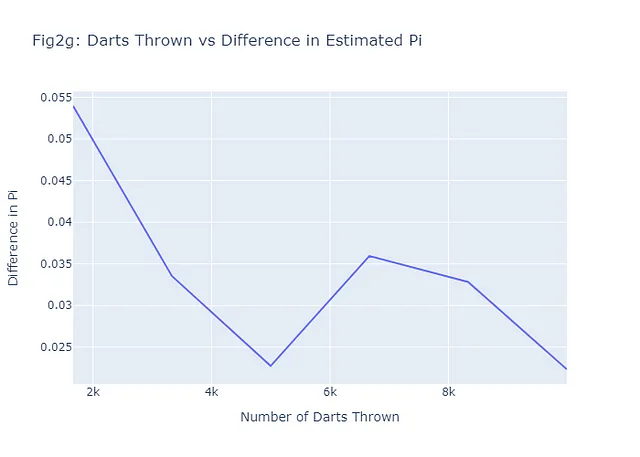
Observa que, incluso con solo 6 ejemplos, el patrón general es el esperado: a medida que se lanzan más dardos (más escenarios), la diferencia entre el valor estimado y el valor real es menor, y por lo tanto, la predicción es mejor.

Supongamos que lanzamos un total de 1,000,000 de dardos y nos permitimos hacer 500 predicciones. En otras palabras, registraremos la diferencia entre los valores estimados y reales de pi en 500 intervalos equidistantes a lo largo de la simulación de 1,000,000 de dardos lanzados. En lugar de generar 500 figuras adicionales, pasemos directamente a lo que estamos tratando de confirmar: si es realmente cierto que a medida que se lanzan más dardos, la diferencia entre nuestro valor predicho de pi y el pi real disminuye. Utilizaremos un gráfico de dispersión (Figura 2h):

#500 Escenarios de Monte Carlo; 1,000,000 de dardos lanzadosimport randomimport mathimport plotly.graph_objects as goimport numpy as np# Número total de dardos a lanzar (1M)num_darts = 1000000darts_in_circle = 0# Número de escenarios a registrar (500)num_scenarios = 500darts_per_scenario = num_darts // num_scenarios# Listas para almacenar los datos de cada escenariodarts_thrown_list = []pi_diff_list = []# Lanzaremos una cantidad de dardosfor i in range(num_darts):    # Generar coordenadas x, y aleatorias entre -1 y 1    x, y = random.uniform(-1, 1), random.uniform(-1, 1)        # Verificar si el dardo está dentro del círculo    # Un dardo está dentro del círculo si la distancia desde el origen (0,0) es menor o igual a 1    if math.sqrt(x**2 + y**2) <= 1:        darts_in_circle += 1    # Si es momento de registrar un escenario    if (i + 1) % darts_per_scenario == 0:        # Estimar pi con el método de Monte Carlo        # La estimación es 4 veces el número de dardos dentro del círculo dividido por el número total de dardos        pi_estimate = 4 * darts_in_circle / (i + 1)        # Registrar la cantidad de dardos lanzados y la diferencia entre los valores estimados y reales de pi        darts_thrown_list.append((i + 1) / 1000)  # Dividir entre 1000 para mostrar en miles        pi_diff_list.append(abs(pi_estimate - math.pi))# Crear un gráfico de dispersión con los datosfig = go.Figure(data=go.Scattergl(x=darts_thrown_list, y=pi_diff_list, mode='markers'))# Actualizar el diseño del gráficofig.update_layout(    title="Fig2h: Diferencia entre Pi Estimado y Pi Real vs. Número de Dardos Lanzados (en miles)",    xaxis_title="Número de Dardos Lanzados (en miles)",    yaxis_title="Diferencia entre Pi Estimado y Pi Real",)# Mostrar el gráficofig.show()# Guardar el gráfico como pngpio.write_image(fig2h, "fig2h.png")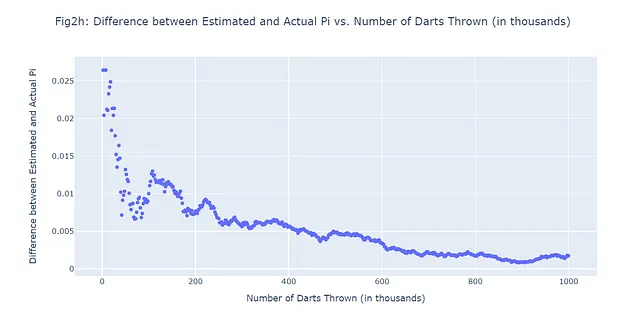

Simulaciones de Monte Carlo y Ajuste de Hiperparámetros: Una Combinación Ganadora

En este punto, es posible que estés pensando: “Monte Carlo es una herramienta estadística interesante, pero ¿cómo se aplica al aprendizaje automático?” La respuesta breve es: de muchas formas. Una de las muchas aplicaciones de las simulaciones de Monte Carlo en el aprendizaje automático se encuentra en el ámbito del ajuste de hiperparámetros.

Los hiperparámetros son los controles y ajustes que nosotros (los humanos) realizamos al configurar algoritmos de aprendizaje automático. Controlan aspectos del comportamiento del algoritmo que, crucialmente, no se aprenden a partir de los datos. Por ejemplo, en un árbol de decisiones, la profundidad máxima del árbol es un hiperparámetro. En una red neuronal, la tasa de aprendizaje y el número de capas ocultas son hiperparámetros.

Elegir los hiperparámetros adecuados puede marcar la diferencia entre un modelo que funciona mal y uno que funciona excelentemente. Pero, ¿cómo sabemos qué hiperparámetros elegir? Aquí es donde entran en juego las simulaciones de Monte Carlo.

Tradicionalmente, los practicantes de aprendizaje automático han utilizado métodos como la búsqueda en cuadrícula o la búsqueda aleatoria para ajustar los hiperparámetros. Estos métodos implican especificar un conjunto de valores posibles para cada hiperparámetro, y luego entrenar y evaluar un modelo para cada combinación posible de hiperparámetros. Esto puede ser computacionalmente costoso y llevar mucho tiempo, especialmente cuando hay muchos hiperparámetros para ajustar o un amplio rango de valores posibles que cada uno puede tomar.

Las simulaciones de Monte Carlo ofrecen una alternativa más eficiente. En lugar de buscar exhaustivamente todas las combinaciones posibles de hiperparámetros, podemos muestrear aleatoriamente el espacio de hiperparámetros según alguna distribución de probabilidad. Esto nos permite explorar el espacio de hiperparámetros de manera más eficiente y encontrar combinaciones buenas de hiperparámetros más rápidamente.

En la próxima sección, utilizaremos un conjunto de datos reales para demostrar cómo usar simulaciones de Monte Carlo para la optimización de hiperparámetros en la práctica. ¡Comencemos!

Simulaciones de Monte Carlo para la Optimización de Hiperparámetros

El Latido de Nuestro Experimento: El Conjunto de Datos de Enfermedades Cardíacas

En el mundo del aprendizaje automático, los datos son la sangre que alimenta nuestros modelos. Para nuestra exploración de las simulaciones de Monte Carlo en la optimización de hiperparámetros, examinemos un conjunto de datos que está cerca del corazón, literalmente. El conjunto de datos de enfermedades cardíacas (CC BY 4.0) del Repositorio de Aprendizaje Automático de la UCI es una colección de registros médicos de pacientes, algunos de los cuales tienen enfermedades cardíacas.

El conjunto de datos contiene 14 atributos, incluyendo edad, sexo, tipo de dolor de pecho, presión arterial en reposo, niveles de colesterol, azúcar en la sangre en ayunas y otros. La variable objetivo es la presencia de enfermedad cardíaca, lo que convierte esto en una tarea de clasificación binaria. Con una mezcla de características categóricas y numéricas, es un conjunto de datos interesante para demostrar la optimización de hiperparámetros.

Primero, echemos un vistazo a nuestro conjunto de datos para tener una idea de con qué vamos a trabajar, siempre es un buen punto de partida.

# Cargar y ver las primeras filas del conjunto de datos
# Importar las bibliotecas necesarias
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score
import numpy as np
import plotly.graph_objects as go

# Cargar el conjunto de datos
# El conjunto de datos está disponible en el Repositorio de Aprendizaje Automático de la UCI
# Es un conjunto de datos sobre enfermedades cardíacas e incluye varias mediciones de pacientes
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/heart-disease/processed.cleveland.data"

# Definir los nombres de las columnas para el marco de datos
column_names = ["edad", "sexo", "cp", "trestbps", "col", "fbs", "restecg", "thalach", "exang", "oldpeak", "slope", "ca", "thal", "objetivo"]

# Cargar el conjunto de datos en un marco de datos de pandas
# Especificamos los nombres de las columnas y también le decimos a pandas que trate '?' como NaN
df = pd.read_csv(url, names=column_names, na_values="?")

# Imprimir las primeras filas del marco de datos
# Esto nos da una visión general rápida de los datos
print(df.head())

Esto nos muestra los primeros cuatro valores en nuestro conjunto de datos en todas las columnas. Si has cargado el archivo csv correcto y has nombrado tus columnas como yo, tu salida se verá como Figura 3.

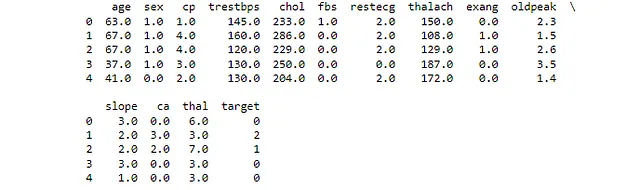
Estableciendo el Pulso: Preprocesamiento de los Datos

Antes de poder usar el conjunto de datos de enfermedades cardíacas para la optimización de hiperparámetros, necesitamos preprocesar los datos. Esto implica varios pasos:

1. Manejo de valores faltantes: Algunos registros en el conjunto de datos tienen valores faltantes. Tendremos que decidir cómo manejar estos valores, ya sea eliminando los registros, completando los valores faltantes o algún otro método.
2. Codificación de variables categóricas: Muchos algoritmos de aprendizaje automático requieren que los datos de entrada sean numéricos. Tendremos que convertir las variables categóricas en un formato numérico.
3. Normalización de características numéricas: Los algoritmos de aprendizaje automático a menudo funcionan mejor cuando las características numéricas están en una escala similar. Aplicaremos normalización para ajustar la escala de estas características.

Comencemos por manejar los valores faltantes. En nuestro conjunto de datos de enfermedades cardíacas, tenemos algunos valores faltantes en las columnas ‘ca’ y ‘thal’. Rellenaremos estos valores faltantes con la mediana de la respectiva columna. Esta es una estrategia común para tratar con datos faltantes, ya que no afecta drásticamente la distribución de los datos.

A continuación, codificaremos las variables categóricas. En nuestro conjunto de datos, las columnas ‘cp’, ‘restecg’, ‘slope’, ‘ca’ y ‘thal’ son categóricas. Utilizaremos la codificación de etiquetas para convertir estas variables categóricas en variables numéricas. La codificación de etiquetas asigna a cada categoría única en una columna un número entero diferente.

Finalmente, normalizaremos las características numéricas. La normalización ajusta la escala de las características numéricas para que todas caigan dentro de un rango similar. Esto puede ayudar a mejorar el rendimiento de muchos algoritmos de aprendizaje automático. Utilizaremos la escala estándar para la normalización, que transforma los datos para que tengan una media de 0 y una desviación estándar de 1.

A continuación se muestra el código de Python que realiza todos estos pasos de preprocesamiento:

# Preprocesamiento
# Importar bibliotecas necesarias
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import LabelEncoder

# Identificar valores faltantes en el conjunto de datos
# Esto imprimirá el número de valores faltantes en cada columna
print(df.isnull().sum())

# Rellenar los valores faltantes con la mediana de la columna
# La clase SimpleImputer de sklearn proporciona estrategias básicas para reemplazar valores faltantes
# Estamos utilizando la estrategia 'mediana', que reemplaza los valores faltantes con la mediana de cada columna
imputer = SimpleImputer(strategy='median')

# Aplicar el imputador al dataframe
# El resultado es un nuevo dataframe donde se han llenado los valores faltantes
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)

# Imprimir las primeras filas del dataframe lleno
# Esto nos da una comprobación rápida para asegurarnos de que la imputación se haya realizado correctamente
print(df_filled.head())

# Identificar variables categóricas en el conjunto de datos
# Estas son variables que contienen datos no numéricos
categorical_vars = df_filled.select_dtypes(include='object').columns

# Codificar variables categóricas
# La clase LabelEncoder de sklearn convierte cada cadena única en un entero único
encoder = LabelEncoder()
for var in categorical_vars:
    df_filled[var] = encoder.fit_transform(df_filled[var])

# Normalizar características numéricas
# La clase StandardScaler de sklearn estandariza las características eliminando la media y escalando a varianzas unitarias
scaler = StandardScaler()

# Aplicar el escalador al dataframe
# El resultado es un nuevo dataframe donde las características numéricas se han normalizado
df_normalized = pd.DataFrame(scaler.fit_transform(df_filled), columns=df_filled.columns)

# Imprimir las primeras filas del dataframe normalizado
# Esto nos da una comprobación rápida para asegurarnos de que la normalización se haya realizado correctamente
print(df_normalized.head())

La primera instrucción de impresión nos muestra el número de valores faltantes en cada columna del conjunto de datos original. En nuestro caso, las columnas ‘ca’ y ‘thal’ tenían algunos valores faltantes.

La segunda instrucción de impresión nos muestra las primeras filas del conjunto de datos después de llenar los valores faltantes. Como se discutió, utilizamos la mediana de cada columna para llenar los valores faltantes.

La tercera instrucción de impresión nos muestra las primeras filas del conjunto de datos después de codificar las variables categóricas. Después de este paso, todas las variables en nuestro conjunto de datos son numéricas.

La última instrucción de impresión nos muestra las primeras filas del conjunto de datos después de normalizar las características numéricas, en las que los datos tendrán una media de 0 y una desviación estándar de 1. Después de este paso, todas las características numéricas en nuestro conjunto de datos están en una escala similar. Verifique que su salida se parezca a Figura 4:

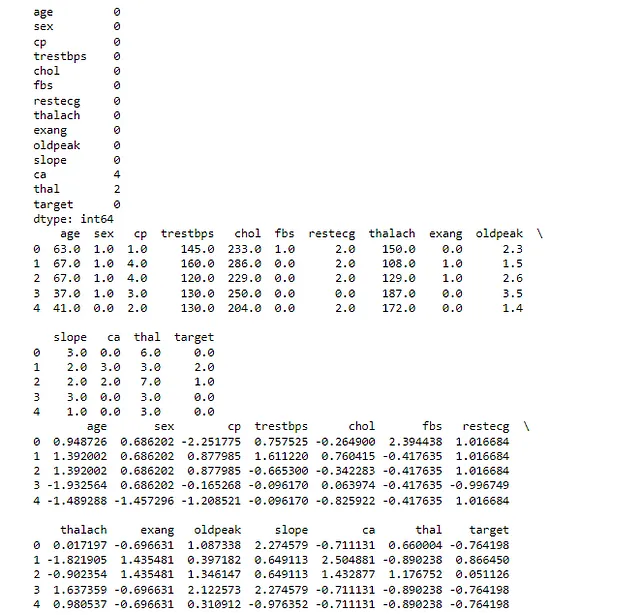
Después de ejecutar este código, tenemos un conjunto de datos preprocesado listo para el modelado.

Implementando un Modelo Básico de Aprendizaje Automático

Ahora que hemos preprocesado nuestros datos, estamos listos para implementar un modelo básico de aprendizaje automático. Este servirá como nuestro modelo de referencia, que luego intentaremos mejorar mediante la sintonización de hiperparámetros.

Utilizaremos un modelo de regresión logística simple para esta tarea. Tenga en cuenta que aunque se llama “regresión”, este es en realidad uno de los algoritmos más populares para problemas de clasificación binaria, como el que estamos tratando en el conjunto de datos de Enfermedad Cardíaca. Es un modelo lineal que predice la probabilidad de la clase positiva.

Después de entrenar nuestro modelo, evaluaremos su rendimiento utilizando dos métricas comunes: precisión y ROC-AUC. La precisión es la proporción de predicciones correctas de todas las predicciones, mientras que el ROC-AUC (Característica de Operación del Receptor – Área Bajo la Curva) mide el equilibrio entre la tasa de verdaderos positivos y la tasa de falsos positivos.

Pero, ¿qué tiene que ver esto con las simulaciones de Monte Carlo? Bueno, los modelos de aprendizaje automático como la regresión logística tienen varios hiperparámetros que se pueden ajustar para mejorar el rendimiento. Sin embargo, encontrar el mejor conjunto de hiperparámetros puede ser como buscar una aguja en un pajar. Aquí es donde entran en juego las simulaciones de Monte Carlo. Al muestrear aleatoriamente diferentes conjuntos de hiperparámetros y evaluar su rendimiento, podemos estimar la distribución de probabilidad de los buenos hiperparámetros y hacer una suposición educada sobre los mejores a usar, de manera similar a cómo elegimos mejores valores de pi en nuestro ejercicio de lanzamiento de dardos.

A continuación se muestra el código de Python que implementa y evalúa un modelo básico de regresión logística para nuestros datos recién preprocesados:

# Modelo de Regresión Logística - Modelo de Referencia
# Importar bibliotecas necesarias
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, roc_auc_score

# Reemplazar la columna 'target' en el DataFrame normalizado con la columna 'target' original
# Esto se hace porque la columna 'target' también se normalizó, lo cual no es lo que queremos
df_normalized['target'] = df['target']

# Binzarizar la columna 'target'
# Esto se hace porque la columna 'target' original contiene valores de 0 a 4
# Queremos simplificar el problema a un problema de clasificación binaria: enfermedad cardíaca o no enfermedad cardíaca
df_normalized['target'] = df_normalized['target'].apply(lambda x: 1 if x > 0 else 0)

# Dividir los datos en conjuntos de entrenamiento y prueba
# La columna 'target' es nuestra etiqueta, por lo que la eliminamos de nuestras características (X)
# Utilizamos un tamaño de prueba del 20%, lo que significa que el 80% de los datos se utilizará para el entrenamiento y el 20% para las pruebas
X = df_normalized.drop('target', axis=1)
y = df_normalized['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Implementar un modelo básico de regresión logística
# La regresión logística es un modelo lineal simple pero potente para problemas de clasificación binaria
model = LogisticRegression()
model.fit(X_train, y_train)

# Realizar predicciones en el conjunto de prueba
# El modelo ha sido entrenado, por lo que ahora podemos usarlo para hacer predicciones en datos no vistos
y_pred = model.predict(X_test)

# Evaluar el modelo
# Utilizamos la precisión (la proporción de predicciones correctas) y el ROC-AUC (una medida de qué tan bien el modelo distingue entre las clases) como nuestras métricas
accuracy = accuracy_score(y_test, y_pred)
roc_auc = roc_auc_score(y_test, y_pred)

# Imprimir las métricas de rendimiento
# Estas nos dan una indicación de qué tan bien está funcionando nuestro modelo
print("Modelo de Referencia " + f'Precisión: {accuracy}')
print("Modelo de Referencia " + f'ROC-AUC: {roc_auc}')

Con una precisión de 0.885 y una puntuación ROC-AUC de 0.884, nuestro modelo básico de regresión logística ha establecido una base sólida para mejorar. Estas métricas indican que nuestro modelo se desempeña bastante bien en distinguir entre pacientes con y sin enfermedad cardíaca. Veamos si podemos mejorarlo.

Ajuste de hiperparámetros con Grid Search

En el aprendizaje automático, a menudo se puede mejorar el rendimiento de un modelo ajustando sus hiperparámetros. Los hiperparámetros son parámetros que no se aprenden de los datos, sino que se establecen antes del inicio del proceso de aprendizaje. Por ejemplo, en la regresión logística, la fuerza de regularización ‘C’ y el tipo de penalización ‘l1’ o ‘l2’ son hiperparámetros.

Vamos a realizar el ajuste de hiperparámetros en nuestro modelo de regresión logística utilizando grid search. Ajustaremos los hiperparámetros ‘C’ y ‘penalty’, y utilizaremos ROC-AUC como nuestra métrica de puntuación. Veamos si podemos superar el rendimiento de nuestro modelo base.

Ahora, vamos a empezar con el código Python para esta sección.

# Grid Search# Importar bibliotecas necesariasfrom sklearn.model_selection import GridSearchCV# Definir los hiperparámetros y sus valores# 'C' es la inversa de la fuerza de regularización (valores más pequeños especifican una regularización más fuerte)# 'penalty' especifica la norma utilizada en la penalización (l1 o l2)hiperparametros = {'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000],                    'penalty': ['l1', 'l2']}# Implementar grid search# GridSearchCV es un método utilizado para ajustar los hiperparámetros de nuestro modelo# Pasamos nuestro modelo, los hiperparámetros a ajustar y el número de pliegues para la validación cruzada# Estamos utilizando ROC-AUC como nuestra métrica de puntuacióngrid_search = GridSearchCV(LogisticRegression(), hiperparametros, cv=5, scoring='roc_auc')grid_search.fit(X_train, y_train)# Obtener los mejores hiperparámetros# GridSearchCV ha encontrado los mejores hiperparámetros para nuestro modelo, así que los imprimimosmejores_hiperparametros = grid_search.best_params_print(f'Mejores hiperparámetros: {mejores_hiperparametros}')# Evaluar el mejor modelo# GridSearchCV también nos da el mejor modelo, así que podemos usarlo para hacer predicciones y evaluar su rendimientomejor_modelo = grid_search.best_estimator_y_pred_mejor = mejor_modelo.predict(X_test)exactitud_mejor = accuracy_score(y_test, y_pred_mejor)roc_auc_mejor = roc_auc_score(y_test, y_pred_mejor)# Imprimir las métricas de rendimiento del mejor modelo# Estos nos dan una indicación de qué tan bien se está desempeñando nuestro modelo después del ajuste de hiperparámetrosprint("Método de Grid Search " + f'Exactitud del mejor modelo: {exactitud_mejor}')print("Método de Grid Search " + f'ROC-AUC del mejor modelo: {roc_auc_mejor}')

Con los mejores hiperparámetros encontrados como {‘C’: 0.1, ‘penalty’: ‘l2’}, nuestra búsqueda en grid tiene una precisión de 0.852 y una puntuación ROC-AUC de 0.853 para el mejor modelo. Curiosamente, este rendimiento es ligeramente inferior al de nuestro modelo base. Esto podría deberse al hecho de que los hiperparámetros de nuestro modelo base ya eran adecuados para este conjunto de datos en particular, o podría ser el resultado de la aleatoriedad inherente en la división entrenamiento-prueba. De todas formas, es un recordatorio valioso de que los modelos y técnicas más complejos no siempre son mejores.

Sin embargo, es posible que también hayas notado que nuestra búsqueda en grid solo exploró una cantidad relativamente pequeña de combinaciones posibles de hiperparámetros. En la práctica, la cantidad de hiperparámetros y sus valores potenciales puede ser mucho mayor, lo que hace que la búsqueda en grid sea computacionalmente costosa o incluso inviable.

Aquí es donde entra en juego el método de Monte Carlo. Veamos si este enfoque más guiado mejora el rendimiento tanto del modelo base original como del modelo basado en búsqueda en grid:

#Monte Carlo# Importar bibliotecas necesariasfrom sklearn.metrics import accuracy_score, roc_auc_scorefrom sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_splitimport numpy as np# Dividir los datos en conjuntos de entrenamiento y pruebaX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# Definir el rango de hiperparámetros# 'C' es la inversa de la fuerza de regularización (valores más pequeños especifican una regularización más fuerte)# 'penalty' especifica la norma utilizada en la penalización (l1 o l2)rango_C = np.logspace(-3, 3, 7)opciones_penalizacion = ['l1', 'l2']# Inicializar variables para almacenar la mejor puntuación y hiperparámetrosmejor_puntuacion = 0mejores_hiperparametros = None# Realizar la simulación de Monte Carlo# Realizaremos 1000 iteraciones. Puedes ajustar este número para ver cómo cambia el rendimiento.# ¡Recuerda la Ley de los Grandes Números!for _ in range(1000):         # Seleccionar hiperparámetros al azar del rango definido    C = np.random.choice(rango_C)    penalizacion = np.random.choice(opciones_penalizacion)        # Crear y evaluar el modelo con estos hiperparámetros    # Estamos utilizando el solucionador 'liblinear' ya que admite tanto regularización L1 como L2    modelo = LogisticRegression(C=C, penalty=penalizacion, solver='liblinear')    modelo.fit(X_train, y_train)    y_pred = modelo.predict(X_test)        # Calcular la exactitud y el ROC-AUC    exactitud = accuracy_score(y_test, y_pred)    roc_auc = roc_auc_score(y_test, y_pred)        # Si este modelo tiene un ROC-AUC mejor hasta ahora, almacenar su puntuación y hiperparámetros    if roc_auc > mejor_puntuacion:        mejor_puntuacion = roc_auc        mejores_hiperparametros = {'C': C, 'penalty': penalizacion}# Imprimir la mejor puntuación y hiperparámetrosprint("Método de Monte Carlo " + f'Mejor ROC-AUC: {mejor_puntuacion}')print("Método de Monte Carlo " + f'Mejores hiperparámetros: {mejores_hiperparametros}')# Entrenar el modelo con los mejores hiperparámetrosmejor_modelo = LogisticRegression(**mejores_hiperparametros, solver='liblinear')mejor_modelo.fit(X_train, y_train)# Hacer predicciones en el conjunto de pruebay_pred = mejor_modelo.predict(X_test)# Calcular e imprimir la exactitud del mejor modeloexactitud = accuracy_score(y_test, y_pred)print("Método de Monte Carlo " + f'Exactitud del mejor modelo: {exactitud}')

En el método de Monte Carlo, encontramos que el mejor puntaje ROC-AUC fue de 0.9014, con los mejores hiperparámetros siendo {‘C’: 0.1, ‘penalty’: ‘l1’}. La precisión del mejor modelo fue de 0.9016.

Parece que Monte Carlo acaba de sacar un as de la baraja, esto es una mejora tanto respecto al modelo base como al modelo ajustado utilizando búsqueda en rejilla. Te animo a ajustar el código Python para ver cómo afecta al rendimiento, recordando los principios discutidos. Intenta mejorar el método de búsqueda en rejilla aumentando el espacio de hiperparámetros, o compara el tiempo de cálculo con el método de Monte Carlo. Aumenta y disminuye el número de iteraciones para nuestro método de Monte Carlo para ver cómo afecta al rendimiento.

Conclusión

El método de Monte Carlo, nacido de un juego de solitario, ha redefinido sin duda el panorama de las matemáticas computacionales y la ciencia de datos. Su poder radica en su simplicidad y versatilidad, permitiéndonos abordar problemas complejos y de alta dimensionalidad con relativa facilidad. Desde estimar el valor de pi con un juego de dardos hasta ajustar hiperparámetros en modelos de aprendizaje automático, las simulaciones de Monte Carlo se han demostrado como una herramienta invaluable en nuestro arsenal de ciencia de datos.

En este artículo, hemos recorrido desde los orígenes del método de Monte Carlo, pasando por sus fundamentos teóricos, hasta sus aplicaciones prácticas en el aprendizaje automático. Hemos visto cómo se puede utilizar para optimizar modelos de aprendizaje automático, mediante una exploración práctica de la sintonización de hiperparámetros utilizando un conjunto de datos del mundo real. También lo hemos comparado con otros métodos, demostrando su eficiencia y efectividad.

Pero la historia de Monte Carlo está lejos de terminar. A medida que continuamos empujando los límites del aprendizaje automático y la ciencia de datos, el método de Monte Carlo sin duda seguirá desempeñando un papel crucial. Ya sea que estemos desarrollando aplicaciones de IA sofisticadas, dando sentido a datos complejos o simplemente jugando un juego de solitario, el método de Monte Carlo es un testimonio del poder de la simulación y la aproximación en la resolución de problemas complejos.

A medida que avanzamos, tomémonos un momento para apreciar la belleza de este método, un método que tiene sus raíces en un simple juego de cartas, pero que tiene el poder de impulsar algunos de los cálculos más avanzados del mundo. El método de Monte Carlo realmente es un juego de alta complejidad y probabilidad, y hasta ahora, parece que siempre gana la casa. Así que sigue barajando las cartas, sigue jugando tus cartas y recuerda: en el juego de la ciencia de datos, Monte Carlo podría ser tu as en la manga.

Pensamientos finales

¡Felicidades por llegar al final! Hemos recorrido el mundo de las probabilidades, luchado con modelos complejos y salido con un nuevo aprecio por el poder de las simulaciones de Monte Carlo. Los hemos visto en acción, simplificando problemas intrincados en componentes manejables e incluso optimizando hiperparámetros para tareas de aprendizaje automático.

Si disfrutas sumergiéndote en las intrincadas soluciones de problemas de aprendizaje automático tanto como yo, sígueme en VoAGI y LinkedIn. Juntos, naveguemos el laberinto de la IA, una solución ingeniosa a la vez.

Hasta nuestra próxima aventura estadística, sigue explorando, sigue aprendiendo y sigue simulando. Y en tu viaje de ciencia de datos y aprendizaje automático, que las probabilidades estén siempre a tu favor.

Nota: Todas las imágenes, a menos que se indique lo contrario, son del autor.

We will continue to update Zepes; if you have any questions or suggestions, please contact us!