Inmersión teórica profunda en la Regresión Lineal

Deep theoretical immersion in Linear Regression.

Aprenda por qué la regresión lineal es como es y cómo extenderla naturalmente de varias maneras

La mayoría de los aspirantes a bloggers de ciencia de datos lo hacen: escriben un artículo introductorio sobre la regresión lineal, y es una elección natural ya que este es uno de los primeros modelos que aprendemos al ingresar al campo. Si bien estos artículos son excelentes para principiantes, la mayoría no profundiza lo suficiente para satisfacer a los científicos de datos senior.

Así que permítanme guiarlos a través de algunos detalles no reconocidos, pero refrescantes, sobre la regresión lineal que los convertirán en un mejor científico de datos (y le darán puntos extras durante las entrevistas).

Este artículo es bastante matemático, así que para seguirlo, es beneficioso tener una base sólida con probabilidades y cálculo.

El proceso de generación de datos

Soy un gran fan de pensar en el proceso de generación de datos al modelar. Las personas que trabajan con modelos bayesianos saben a lo que me refiero, pero para los demás: imaginen que tienen un conjunto de datos (X, y) que consiste en muestras (x, y). Dado x, ¿cómo se llega a un objetivo y?

• Conoce BITE Un Nuevo Método Que Reconstruye la Forma y Poses 3D de un Perro a Partir de una Imagen, Incluso con Poses Desafiantes como Sentado y Acostado.
• Conoce Paella Un Nuevo Modelo de IA Similar a Difusión que Puede Generar Imágenes de Alta Calidad Mucho Más Rápido que Usando Difusión Estable.
• Usando ChatGPT para Debugging Eficiente

Supongamos que tenemos n puntos de datos y que cada x tiene k componentes/características.

Para un modelo lineal con los parámetros w₁, …, wₖ (coeficientes), b (intersección), σ (ruido), se asume que el proceso de generación de datos se ve así:

1. Calcular µ = w₁x₁ + w₂x₂ +…+ wₖxₖ + b.
2. Lanzar un número aleatorio y ~ N(µ, σ²). Esto es independiente de otros números generados al azar. Alternativamente: Lanzar ε ~ N(0, σ²) y producir y = µ + ε .

Es todo. Estas dos simples líneas son equivalentes a las suposiciones más importantes de la regresión lineal que a la gente le gusta explicar en gran detalle, es decir, linealidad, homocedasticidad e independencia de errores.

A partir del paso 1. del proceso, también se puede ver que modelamos la expectativa µ con la ecuación lineal típica w₁x₁ + w₂x₂ +…+ wₖxₖ + b en lugar del objetivo real. Sabemos que de todos modos no alcanzaremos el objetivo, por lo que nos conformamos con la media de la distribución que genera y.

Extensiones

Modelos lineales generalizados. No estamos obligados a usar una distribución normal para el proceso de generación. Si tratamos con un conjunto de datos que solo contiene objetivos positivos, puede ser beneficioso asumir que se utiliza una distribución de Poisson Poi(µ) en lugar de una distribución normal. Esto le da una regresión de Poisson.

Si nuestro conjunto de datos solo tiene los objetivos 0 y 1, use una distribución de Bernoulli Ber(p), donde p = sigmoide(µ), et voilà: tiene regresión logística.

¿Solo números entre 0, 1,…, n? Use una distribución binomial para obtener regresión binomial.

La lista continúa. En resumen:

Piense en qué distribución podría haber generado las etiquetas que observa en los datos.

¿Qué estamos minimizando realmente?

Bien, entonces decidimos sobre un modelo. ¿Cómo lo entrenamos ahora? ¿Cómo aprendemos los parámetros? Por supuesto, lo sabes: minimizamos el error cuadrático (medio). ¿Pero por qué?

El secreto es que simplemente haces una estimación de máxima verosimilitud utilizando el proceso de generación que describimos anteriormente. Las etiquetas que observamos son y₁, y₂,…, yₙ, todas ellas generadas de manera independiente a través de una distribución normal con medios µ₁, µ₂,…, µₙ. ¿Cuál es la probabilidad de ver estas y? Es:

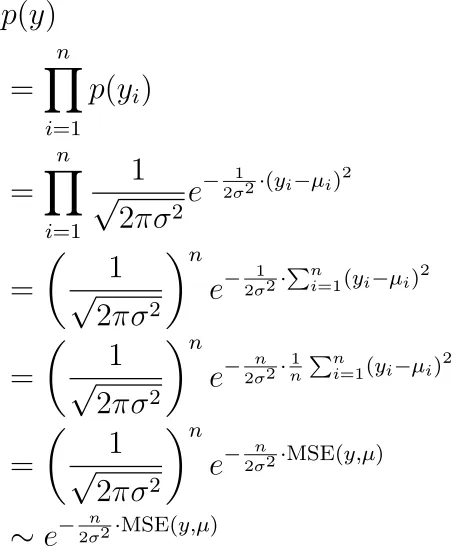
Ahora queremos encontrar los parámetros (que están ocultos en los µᵢ) para maximizar este término. Esto es equivalente a minimizar el error cuadrático medio, como se puede ver.

Extensiones

Varianzas desiguales. De hecho, σ no tiene que ser constante. Puedes tener un σᵢ diferente para cada observación en tu conjunto de datos. Entonces, en lugar de eso, minimizarías

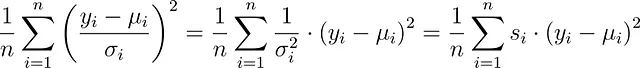
que es mínimos cuadrados con pesos de muestra s. Las bibliotecas de modelado normalmente permiten establecer estos pesos. En scikit-learn, por ejemplo, puedes establecer la palabra clave sample_weight en la función fit.

De esta manera, puedes poner más énfasis en ciertas observaciones aumentando el s correspondiente. Esto es equivalente a disminuir la varianza σ², es decir, estás más seguro de que el error para esta observación es menor. Este método también se llama mínimos cuadrados ponderados.

Varianzas que dependen de la entrada. Incluso puedes decir que la varianza también depende de la entrada x. En este caso, obtienes la interesante función de pérdida que también se llama atenuación de la varianza:

Todo el proceso de derivación se describe aquí:

Obtén estimaciones de incertidumbre en redes neuronales de regresión de forma gratuita

Dada la función de pérdida adecuada, una red neuronal estándar también puede generar incertidumbre

towardsdatascience.com

Regularización. En lugar de solo maximizar la probabilidad de las etiquetas observadas y₁, y₂, …, yₙ, puedes adoptar un punto de vista bayesiano y maximizar la verosimilitud a posteriori

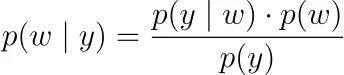
Aquí, p ( y | w ) es la función de verosimilitud de arriba. Tenemos que decidir sobre una densidad de probabilidad para p ( w ), una llamada prior o distribución previa. Si decimos que los parámetros están distribuidos normalmente de forma independiente alrededor de 0, es decir, wᵢ ~ N(0, ν²), entonces terminamos con regularización L2, es decir, regresión de cresta. Para una distribución de Laplace, recuperamos regularización L1, es decir, LASSO.

¿Por qué es eso? Usemos la distribución normal como ejemplo. Tenemos

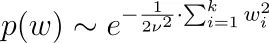
así que junto con nuestra fórmula para p ( y | w ) de arriba, tenemos que maximizar

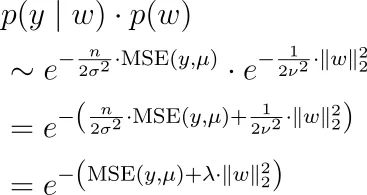
lo que significa que tenemos que minimizar el error cuadrático medio más algún hiperparámetro de regularización multiplicado por la norma L2 de w.

Tenga en cuenta que hemos eliminado el denominador p ( y ) de la fórmula de Bayes ya que no depende de w, por lo que podemos ignorarlo para la optimización.

Puede utilizar cualquier otra distribución previa para sus parámetros para crear regularizaciones más interesantes. Incluso puede decir que sus parámetros w tienen una distribución normal pero correlacionados con alguna matriz de correlación Σ.

Supongamos que Σ es definida positiva, es decir, estamos en el caso no degenerado. De lo contrario, no hay densidad p ( w ).

Si hace los cálculos, encontrará que entonces debemos optimizar

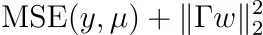
para alguna matriz Γ. Nota: Γ es invertible y tenemos Σ⁻¹ = ΓᵀΓ. Esto también se llama regularización de Tikhonov.

Sugerencia: comience con el hecho de que

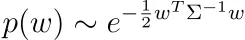
y recuerde que las matrices definidas positivas pueden descomponerse en un producto de alguna matriz invertible y su transpuesta.

Minimizar la Función de Pérdida

Genial, entonces definimos nuestro modelo y sabemos lo que queremos optimizar. ¿Pero cómo podemos optimizarlo, es decir, aprender los mejores parámetros que minimicen la función de pérdida? ¿Y cuándo hay una solución única? Averigüémoslo.

Mínimos Cuadrados Ordinarios

Supongamos que no regularizamos ni usamos pesos de muestra. Entonces, el MSE se puede escribir como

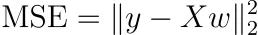
Esto es bastante abstracto, así que escribámoslo de manera diferente como

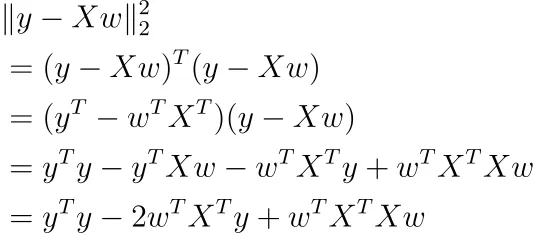
Usando cálculo matricial, puede tomar la derivada de esta función con respecto a w (asumimos que el término de sesgo b está incluido allí).

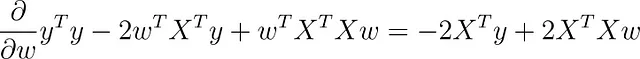
Si establece este gradiente en cero, obtiene

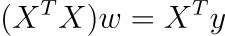
Si la matriz ( n × k )-X tiene un rango de k, también lo tiene la matriz ( k × k )-XᵀX, es decir, es invertible. ¿Por qué? Se sigue de rank( X ) = rank( XᵀX ) .

En este caso, obtenemos la solución única

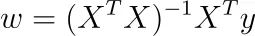
Nota: Los paquetes de software no optimizan de esta manera, sino que utilizan descenso de gradiente u otras técnicas iterativas porque es más rápido. Aún así, la fórmula es agradable y nos da algunas ideas de alto nivel sobre el problema.

Pero, ¿es realmente un mínimo? Podemos averiguarlo calculando el Hessiano, que es X ᵀ X. La matriz es semidefinida positiva ya que w ᵀ X ᵀ Xw = |Xw|² ≥ 0 para cualquier w. Es incluso estrictamente definida positiva ya que X ᵀ X es invertible, es decir, 0 no es un eigenvector, por lo que nuestro w óptimo realmente minimiza nuestro problema.

Multicolinealidad perfecta

Ese fue el caso amistoso. Pero, ¿qué sucede si X tiene un rango menor que k? Esto puede suceder si tenemos dos características en nuestro conjunto de datos donde una es un múltiplo de la otra, por ejemplo, usamos las características altura (en m) y altura (en cm) en nuestro conjunto de datos. Entonces tenemos altura (en cm) = 100 * altura (en m).

También puede suceder si codificamos datos categóricos y no eliminamos una de las columnas. Por ejemplo, si tenemos una característica de color en nuestro conjunto de datos que puede ser rojo, verde o azul, entonces podemos codificar uno a uno y terminar con tres columnas color_rojo, color_verde y color_azul. Para estas características, tenemos color_rojo + color_verde + color_azul = 1, lo que induce una multicolinealidad perfecta también.

En estos casos, el rango de X ᵀ X también es menor que k, por lo que esta matriz no es invertible.

Fin de la historia.

¿O no? En realidad, no, porque puede significar dos cosas: ( X ᵀ X ) w = X ᵀ y tiene

1. no solución o
2. infinitas soluciones.

Resulta que en nuestro caso, podemos obtener una solución usando la inversa de Moore-Penrose. Esto significa que estamos en el caso de infinitas soluciones, todas ellas dándonos la misma pérdida de error cuadrático medio (entrenamiento).

Si denotamos la inversa de Moore-Penrose de A por A⁺, podemos resolver el sistema de ecuaciones lineales como

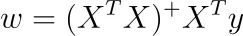
Para obtener las otras infinitas soluciones, simplemente agregue el espacio nulo de X ᵀ X a esta solución específica.

Minimización con regularización de Tikhonov

Recuerde que podríamos agregar una distribución previa a nuestros pesos. Luego tuvimos que minimizar

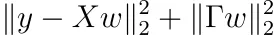
para alguna matriz invertible Γ. Siguiendo los mismos pasos que en el método de mínimos cuadrados ordinarios, es decir, tomando la derivada con respecto a w y estableciendo el resultado en cero, la solución es

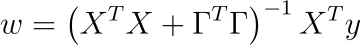
La parte interesante:

¡XᵀX + ΓᵀΓ siempre es invertible!

Averigüemos por qué. Basta con demostrar que el espacio nulo de X ᵀ X + ΓᵀΓ es solo {0}. Entonces, tomemos un w con ( X ᵀ X + ΓᵀΓ) w = 0. Ahora, nuestro objetivo es demostrar que w = 0.

De ( X ᵀ X + ΓᵀΓ) w = 0 se sigue que

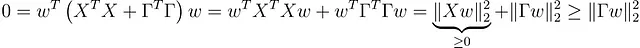
lo que a su vez implica |Γ w | = 0 → Γ w = 0. Como Γ es invertible, w debe ser 0. Usando el mismo cálculo, podemos ver que el Hessiano también es definido positivo.

¡Genial, la regularización de Tikhonov ayuda automáticamente a hacer que la solución sea única! Dado que la regresión de Ridge es un caso especial de la regresión de Tikhonov (para Γ = λ Iₖ, Iₖ es la matriz de identidad k-dimensional), lo mismo se aplica allí.

Agregar pesos de muestra

Por último, agreguemos pesos de muestra a la regularización de Tikhonov. Agregar pesos de muestra es equivalente a minimizar

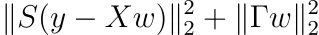
Para alguna matriz diagonal S con entradas diagonales positivas sᵢ. Minimizar es tan sencillo como en el caso de las mínimas cuadráticas ordinarias. El resultado es

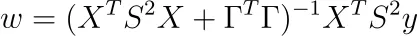
Nota: La Hessiana también es definida positiva.

Tarea para ti

Suponga que para la regularización de Tikhonov, no imponemos que los pesos deben centrarse en 0, sino en algún otro punto w₀. Muestre que el problema de optimización se convierte en

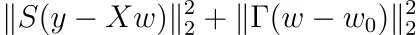
y que la solución es

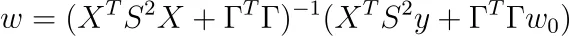
Esta es la forma más general de la regularización de Tikhov. Algunas personas prefieren definir P := S², Q := ΓᵀΓ, como se hace aquí.

Conclusión

En este artículo, te llevé en un viaje a través de varios aspectos avanzados de la regresión lineal. Al adoptar una visión generativa, pudimos ver que los modelos lineales generalizados solo difieren de los modelos lineales normales en el tipo de distribución que se utiliza para muestrear el objetivo y.

Luego vimos que minimizar el error cuadrático medio es equivalente a maximizar la probabilidad de los valores observados. Si imponemos una distribución normal previa en los parámetros aprendibles, terminamos con la regularización de Tikhonov (y L2 como un caso especial). También podemos usar diferentes distribuciones previas como la distribución Laplace, pero entonces ya no hay fórmulas de solución cerradas. Aún así, los enfoques de programación convexa también te permiten encontrar los mejores parámetros.

Como último paso, encontramos muchas fórmulas de solución directa para cada problema de minimización considerado. Estas fórmulas generalmente no se usan en la práctica para conjuntos de datos grandes, pero pudimos ver que las soluciones son siempre únicas. Y también aprendimos a hacer algunos cálculos en el camino. 😉

Espero que hayas aprendido algo nuevo, interesante y valioso hoy. ¡Gracias por leer!

Como último punto, si

1. quieres apoyarme en escribir más sobre aprendizaje automático y
2. planeas obtener una suscripción de Zepes de todos modos,

¿por qué no hacerlo a través de este enlace ? ¡Esto me ayudaría mucho! 😊

Para ser transparente, el precio para ti no cambia, pero alrededor de la mitad de las tarifas de suscripción van directamente a mí.

¡Muchas gracias si consideras apoyarme!

Si tienes alguna pregunta, escríbeme en LinkedIn !

We will continue to update Zepes; if you have any questions or suggestions, please contact us!