Una Inmersión Profunda en la Ciencia de la Expectativa Estadística

A Deep Dive into the Science of Statistical Expectation

Cómo llegamos a esperar algo, lo que significa esperar cualquier cosa y las matemáticas que dan lugar al significado.

Fue el verano de 1988 cuando pisé un barco por primera vez en mi vida. Era un ferry de pasajeros desde Dover, Inglaterra, hasta Calais, Francia. No lo sabía entonces, pero estaba viviendo el final de la era dorada de los cruces del Canal por ferry. Esto fue justo antes de que las aerolíneas de bajo costo y el Túnel del Canal casi arruinaran lo que todavía creo que es la mejor manera de hacer ese viaje.

Esperaba que el ferry se pareciera a uno de los muchos barcos que había visto en libros para niños. En cambio, me encontré con un rascacielos imposiblemente grande y reluciente de color blanco con pequeñas ventanas cuadradas. Y el rascacielos parecía estar descansando de costado por alguna razón desconcertante. Desde mi ángulo de visión en el muelle, no pude ver el casco ni las chimeneas del barco. Todo lo que vi fue su exterior largo, plano y acristalado. Estaba mirando un rascacielos horizontal.

Pensando en retrospectiva, es divertido reinterpretar mi experiencia en el lenguaje de las estadísticas. Mi cerebro había calculado la forma esperada de un ferry a partir de la muestra de datos de imágenes de barcos que había visto. Pero mi muestra era lamentablemente poco representativa de la población, lo que hacía que la media de la muestra fuera igualmente poco representativa de la media de la población. Estaba intentando decodificar la realidad utilizando una media de muestra muy sesgada.

Mareo

Este viaje por el Canal también fue la primera vez que me mareé. Dicen que cuando te mareas en un barco, debes salir a la cubierta, respirar el aire fresco y fresco del mar y mirar el horizonte. Lo único que realmente funciona para mí es sentarme, cerrar los ojos y beber mi refresco favorito hasta que mis pensamientos se alejen lentamente de la náusea desgarradora que me revuelve el estómago. Por cierto, no me estoy alejando lentamente del tema de este artículo. Me adentraré en las estadísticas en un minuto. Mientras tanto, permítanme explicar mi comprensión de por qué te mareas en un barco para que veas la conexión con el tema en cuestión.

• Costo del Desarrollo de IA Conversacional en el Sistema Bancario en el 2023
• David Autor nombrado Científico Distinguido NOMIS 2023
• Los mejores 6 ETFs de Inteligencia Artificial (IA) en 2023.

En la mayoría de los días de tu vida, no te estás balanceando en un barco. En tierra firme, cuando inclinas tu cuerpo hacia un lado, tus oídos internos y cada músculo de tu cuerpo le dicen a tu cerebro que te estás inclinando hacia un lado. ¡Sí, tus músculos también hablan con tu cerebro! Tus ojos secundan ansiosamente todos estos comentarios y todo sale bien. Pero en un barco, todo el infierno se desata en este pacto afable entre ojo y oído.

En un barco, cuando el mar hace que el barco se incline, se balancee, se balancee, se balancee, se desplace, se balancee o haga cualquier otra cosa, lo que tus ojos le dicen a tu cerebro puede ser notablemente diferente de lo que tus músculos y oído interno le dicen a tu cerebro. Tu oído interno podría decir: “Cuidado. Te estás inclinando hacia la izquierda. Deberías ajustar tu expectativa de cómo aparecerá tu mundo”. Pero tus ojos están diciendo: “¡Tonterías! La mesa en la que estoy sentado parece perfectamente nivelada para mí, al igual que el plato de comida que descansa sobre ella. La imagen en la pared de esa cosa que está gritando también parece recta y nivelada. No escuches al oído interno”.

Tus ojos también podrían reportar algo aún más confuso a tu cerebro, como “Sí, te estás inclinando, pero la inclinación no es tan significativa o rápida como tus oídos internos excesivamente entusiastas podrían hacerte creer”.

Es como si tus ojos y tus oídos internos estuvieran pidiéndole cada uno a tu cerebro que creara dos expectativas diferentes sobre cómo va a cambiar tu mundo. Obviamente, tu cerebro no puede hacer eso. Se confunde. Y por razones enterradas en la evolución, tu estómago expresa un fuerte deseo de vaciar su contenido.

Intentemos explicar esta situación lamentable utilizando el marco del razonamiento estadístico. Esta vez, usaremos un poco de matemáticas para ayudar en nuestra explicación.

¿Deberías esperar marearte? Adentrándonos en las estadísticas del mareo

Definamos una variable aleatoria X que toma dos valores: 0 y 1. X es 0 si las señales de tus ojos no concuerdan con las señales de tus oídos internos. X es 1 si concuerdan:

En teoría, cada valor de X debe llevar una cierta probabilidad P( X =x). Las probabilidades P( X =0) y P( X =1) juntas constituyen la Función de Masa de Probabilidad de X. Lo expresamos de la siguiente manera:

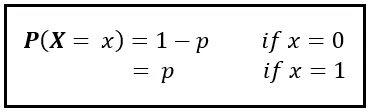
La mayoría de las veces, las señales de tus ojos concordarán con las señales de tus oídos internos. Entonces, p es casi igual a 1, y (1 – p) es un número realmente, realmente pequeño.

Vamos a hacer una suposición salvaje sobre el valor de (1 – p). Usaremos la siguiente línea de razonamiento para llegar a una estimación: Según las Naciones Unidas, la esperanza de vida promedio de los humanos al nacer en 2023 es de aproximadamente 73 años. En segundos, eso corresponde a 2302128000 (alrededor de 2.3 mil millones). Supongamos que un individuo promedio experimenta mareo por mar durante 16 horas en su vida, lo que equivale a 28800 segundos. Ahora no discutamos sobre las 16 horas. ¿Recuerdas que es una suposición salvaje? Entonces, 28800 segundos nos da una estimación de trabajo de (1 – p) de 28000/2302128000 = 0.0000121626 y p=(1 – 0.0000121626) = 0.9999878374. Así que durante cualquier segundo de la vida promedio de una persona, la probabilidad incondicional de que experimente mareo por mar es solo del 0.0000121626.

Con estas probabilidades, ejecutaremos una simulación que durará mil millones de segundos en la vida de un cierto John Doe. Eso es alrededor del 50% de la vida simulada de JD. JD prefiere pasar la mayor parte de este tiempo en tierra firme. Toma el ocasional crucero por el mar en el que a menudo se marea. Simularemos si J experimentará mareo por mar durante cada uno de los mil millones de segundos de la simulación. Para hacerlo, realizaremos mil millones de pruebas de una variable aleatoria de Bernoulli que tiene probabilidades de p y (1 – p). El resultado de cada prueba será 1 si J se marea, o 0 si no se marea. Al realizar este experimento, obtendremos mil millones de resultados. También puedes ejecutar esta simulación usando el siguiente código de Python:

import numpy as npp = 0.9999878374num_trials = 1000000000outcomes = np.random.choice([0, 1], size=num_trials, p=[1 - p, p])

Contemos el número de resultados de valor 1 (=no mareado) y 0 (=mareado):

num_outcomes_in_which_not_seasick = sum(outcomes)num_outcomes_in_which_seasick = num_trials - num_outcomes_in_which_not_seasick

Imprimiremos estas cuentas. Cuando las imprimí, obtuve los siguientes valores. Es posible que obtenga resultados ligeramente diferentes cada vez que ejecute su simulación:

num_outcomes_in_which_not_seasick= 999987794num_outcomes_in_which_seasick= 12206

Ahora podemos calcular si JD debería esperar sentirse mareado durante cualquiera de esos mil millones de segundos.

La expectativa se calcula como el promedio ponderado de los dos posibles resultados: uno y cero, siendo los pesos las frecuencias de los dos resultados. Entonces, realicemos este cálculo:

El resultado esperado es de 0.999987794, lo que es prácticamente 1.0. Las matemáticas nos dicen que durante cualquier segundo elegido al azar en los mil millones de segundos de la existencia simulada de JD, JD no debería esperar marearse. Los datos parecen casi prohibirlo.

Ahora juguemos un poco con la fórmula anterior. Comenzaremos reorganizándola de la siguiente manera:

Cuando se reorganiza de esta manera, se ve que surge una subestructura encantadora. Las relaciones en los dos corchetes representan las probabilidades asociadas con los dos resultados, específicamente las probabilidades de muestra derivadas de nuestra muestra de datos de mil millones, en lugar de las probabilidades poblacionales. Son probabilidades de muestra porque las calculamos usando los datos de nuestra muestra de datos de mil millones. Dicho esto, los valores 0.999987794 y 0.000012206 deberían estar bastante cerca de los valores poblacionales de p y (1-p) respectivamente.

Al introducir las probabilidades, podemos reformular la fórmula para la expectativa de la siguiente manera:

Observe que se utilizó la notación para la expectativa, que es E(). Dado que X es una variable aleatoria Bernoulli(p), la fórmula anterior también nos muestra cómo calcular el valor esperado de una variable aleatoria Bernoulli. El valor esperado de X ~ Bernoulli(p) es simplemente p.

De medias de muestra, medias poblacionales y una palabra que te hace sonar genial

E(X) también se llama la media poblacional, denotada por μ, porque utiliza las probabilidades p y (1-p) que son los valores de probabilidad a nivel de población. Estas son las probabilidades “verdaderas” que observará si tuviera acceso a toda la población de valores, lo cual es prácticamente imposible. Los estadísticos usan la palabra “asintótico” al referirse a estas y medidas similares. Se les llama asintóticos porque su significado es significativo solo cuando algo, como el tamaño de la muestra, se acerca al infinito o al tamaño de toda la población. Ahora aquí está la cosa: Creo que a la gente simplemente le gusta decir “asintótico”. Y también creo que es una cobertura conveniente para la problemática verdad de que nunca puedes medir el valor exacto de nada.

En el lado positivo, la imposibilidad de poner tus manos en la población es “el gran nivelador” en el campo de la ciencia estadística. Ya sea que seas un recién graduado o un laureado en Economía, esa puerta a la “población” permanece firmemente cerrada para ti. Como estadístico, te limitas a trabajar con la muestra cuyas deficiencias debes sufrir en silencio. Pero no es realmente un estado de cosas tan malo como suena. Imagina lo que sucederá si comenzaras a conocer los valores exactos de las cosas. Si tuvieras acceso a la población. Si pudieras calcular la media, la mediana y la varianza con precisión. Si pudieras predecir el futuro con precisión milimétrica. Habría poca necesidad de estimar cualquier cosa. Grandes ramas de la estadística dejarían de existir. El mundo necesitaría cientos de miles menos de estadísticos, sin mencionar a los científicos de datos. Imagina el impacto en el desempleo, en la economía mundial, en la paz mundial…

Pero divago. Mi punto es que si X es Bernoulli(p), entonces para calcular E( X ), no puedes usar los valores reales de la población de p y (1 — p). En su lugar, debes conformarte con estimaciones de p y (1 — p). Estas estimaciones las calcularás utilizando no toda la población — ninguna posibilidad de hacer eso. En cambio, lo harás, en la mayoría de los casos, utilizando una muestra de datos de tamaño modesto. Y así, con mucho pesar, debo informarte que lo mejor que puedes hacer es obtener una estimación del valor esperado de la variable aleatoria X. Siguiendo la convención, denotamos la estimación de p como p_hat (p con una pequeña gorra o sombrero encima) y denotamos el valor esperado estimado como E_cap( X ).

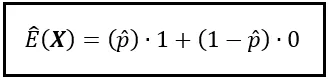
Dado que E_cap( X ) utiliza probabilidades de muestra, se le llama media muestral. Se denota como x̄ o ‘x barra’. Es una x con una barra colocada en su cabeza.

La media poblacional y la media muestral son el Batman y Robin de la estadística.

Gran parte de la estadística está dedicada a calcular la media muestral y a utilizarla como una estimación de la media poblacional.

Y ahí lo tienes — la amplia expansión de la estadística resumida en una sola frase. 😉

Zambullirse en lo profundo de la expectativa

Nuestro experimento mental con la variable aleatoria Bernoulli ha sido instructivo en el sentido de que ha desentrañado en cierta medida la naturaleza de la expectativa. La variable Bernoulli es una variable binaria, y fue fácil de trabajar. Sin embargo, las variables aleatorias con las que a menudo trabajamos pueden tomar muchos valores diferentes. Afortunadamente, podemos extender fácilmente el concepto y la fórmula de la expectativa a variables aleatorias de muchos valores. Veámoslo con otro ejemplo.

El valor esperado de una variable aleatoria discreta de múltiples valores

La siguiente tabla muestra un subconjunto de un conjunto de datos de información sobre 205 automóviles. Específicamente, la tabla muestra el número de cilindros dentro del motor de cada vehículo.

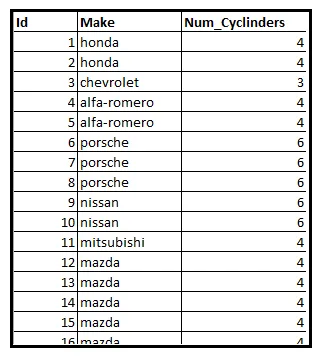
Sea Y una variable aleatoria que contiene el número de cilindros de un vehículo elegido al azar de este conjunto de datos. Sabemos que el conjunto de datos contiene vehículos con recuentos de cilindros de 2, 3, 4, 5, 6, 8 o 12. Por lo tanto, el rango de Y es el conjunto E=[2, 3, 4, 5, 6, 8, 12].

Agruparemos las filas de datos por recuento de cilindros. La tabla siguiente muestra los recuentos agrupados. La última columna indica la correspondiente probabilidad de muestra de ocurrencia de cada recuento. Esta probabilidad se calcula dividiendo el tamaño del grupo por 205:

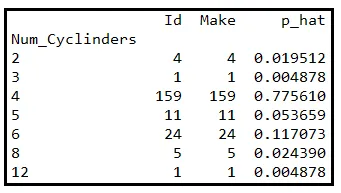
Utilizando las probabilidades de muestra, podemos construir la Función de Masa de Probabilidad P( Y ) para Y. Si la representamos gráficamente frente a Y, se ve así:

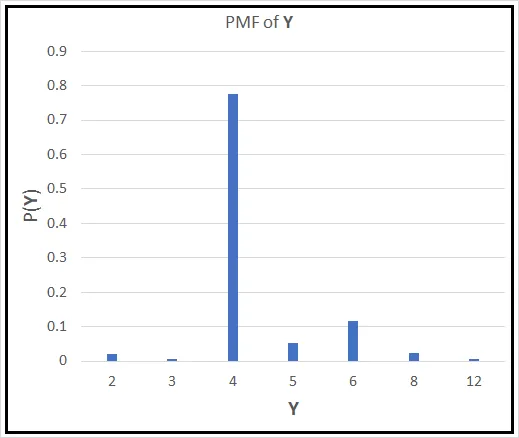
Si un vehículo elegido al azar se pone delante de ti, ¿qué esperas que sea su número de cilindros? Solo con mirar la PMF, el número que querrás adivinar es 4. Sin embargo, hay matemáticas frías y duras respaldando esta suposición. Similar al Bernoulli X , puedes calcular el valor esperado de Y de la siguiente manera:

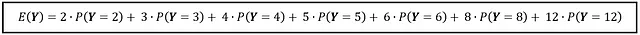
Si calculas la suma, asciende a 4.38049, lo cual es bastante cercano a tu suposición de 4 cilindros.

Dado que el rango de Y es el conjunto E= [2,3,4,5,6,8,12], podemos expresar esta suma como una suma sobre E de la siguiente manera:

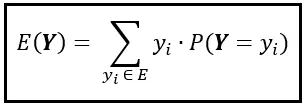
Puedes usar la fórmula anterior para calcular el valor esperado de cualquier variable aleatoria discreta cuyo rango sea el conjunto E .

El valor esperado de una variable aleatoria continua

Si estás lidiando con una variable aleatoria continua, la situación cambia un poco, como se describe a continuación.

Volviendo a nuestro conjunto de datos de vehículos. Específicamente, veamos las longitudes de los vehículos:

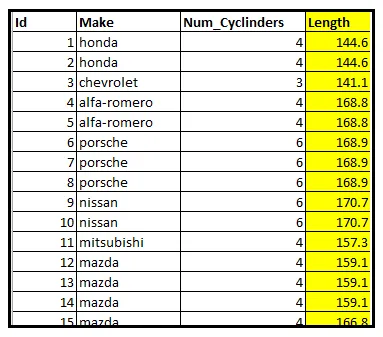
Supongamos que Z es la longitud en pulgadas de un vehículo seleccionado al azar. El rango de Z ya no es un conjunto discreto de valores. En lugar de eso, es un subconjunto del conjunto ℝ de números reales. Dado que las longitudes son siempre positivas, es el conjunto de todos los números reales positivos, denotado como ℝ >0.

Dado que el conjunto de todos los números reales positivos tiene un número (incontable) infinito de valores, no tiene sentido asignar una probabilidad a un valor individual de Z . Si no me crees, considera un rápido experimento mental: Imagina asignar una probabilidad positiva a cada posible valor de Z . Te darás cuenta de que las probabilidades sumarán infinitamente, lo cual es absurdo. Por lo tanto, la probabilidad P( Z =z) simplemente no existe. En su lugar, debes trabajar con la Función de Densidad de Probabilidad f( Z =z) que asigna una densidad de probabilidad a diferentes valores de Z .

Anteriormente discutimos cómo calcular el valor esperado de una variable aleatoria discreta usando la Función de Masa de Probabilidad.

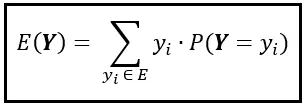
¿Podemos reutilizar esta fórmula para variables aleatorias continuas? La respuesta es sí. Para saber cómo, imagínate con un microscopio electrónico.

Toma ese microscopio y enfócalo en el rango de Z que es el conjunto de todos los números reales positivos ( ℝ >0). Ahora, acércate a un intervalo imposiblemente pequeño (z, z+δz], dentro de este rango. A esta escala microscópica, podrías observar que, para todos los propósitos prácticos (ahora, ¿no es ese un término útil?), la densidad de probabilidad f( Z =z) es constante a través de δz. En consecuencia, el producto de f( Z =z) y δz puede aproximar la probabilidad de que la longitud de un vehículo seleccionado al azar caiga dentro del intervalo abierto-cerrado (z, z+δz].

Armado con esta probabilidad aproximada, puedes aproximar el valor esperado de Z de la siguiente manera:

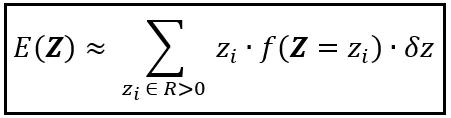
Observa cómo saltamos de la fórmula para E( Y ) a esta aproximación. Para llegar a E( Z ) desde E( Y ), hicimos lo siguiente:

• Reemplazamos el y_i discreto con el z_i de valor real.
• Reemplazamos P( Y =y), que es la PMF de Y, con f( Z =z)δz, que es la probabilidad aproximada de encontrar z en el intervalo microscópico (z, z+δz].
• En lugar de sumar sobre el rango discreto y finito de Y, que es E, sumamos sobre el rango continuo e infinito de Z, que es ℝ >0.
• Finalmente, reemplazamos el signo de igualdad con el signo de aproximación. Y ahí radica nuestra culpabilidad. Hicimos trampa. Colamos la probabilidad f( Z =z)δz como una aproximación de la probabilidad exacta P( Z =z). Hicimos trampa porque la probabilidad exacta, P( Z =z), no puede existir para un Z continuo. Debemos enmendar esta transgresión, que es exactamente lo que haremos a continuación.

Ahora ejecutamos nuestra obra maestra, nuestra pièce de résistance, y al hacerlo, nos redimimos.

Dado que ℝ >0 es el conjunto de números reales positivos, hay un número infinito de intervalos de microscopio de tamaño δz en ℝ >0. Por lo tanto, la suma sobre ℝ >0 es una suma sobre un número infinito de términos. Este hecho nos presenta la oportunidad perfecta para reemplazar la suma aproximada por una integral exacta, como sigue:

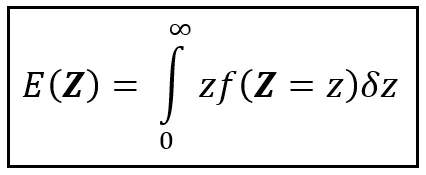
En general, si el rango de Z es el intervalo de valores reales [a, b], establecemos los límites de la integral definida en a y b en lugar de 0 y ∞.

Si conoces la PDF de Z y si la integral de z veces f( Z =z) existe sobre [a, b], resolverás la integral anterior y obtendrás E( Z ) por tus problemas.

Si Z está uniformemente distribuido en el rango [a, b], su PDF es la siguiente:

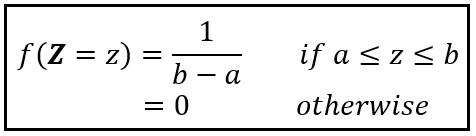
Si estableces a=1 y b=5,

f( Z =z) = 1/(5–1) = 0.25.

La densidad de probabilidad es constante en 0.25 desde Z =1 hasta Z =5 y es cero en cualquier otro lugar. Así es como se ve la PDF de Z:

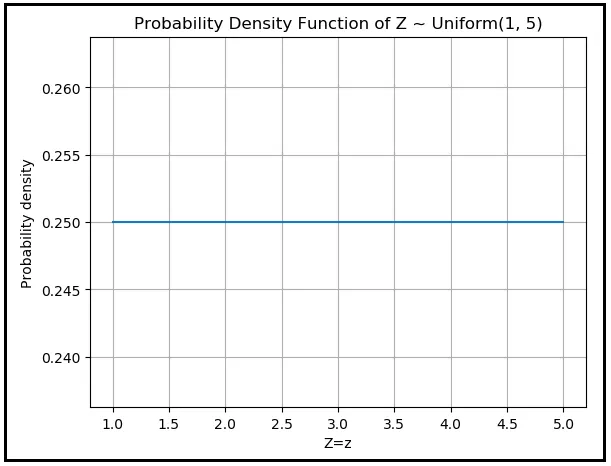
Básicamente es una línea horizontal continua y plana desde (1,0.25) hasta (5,0.25) y es cero en cualquier otro lugar.

En general, si la densidad de probabilidad de Z está uniformemente distribuida en el intervalo [a, b], la PDF de Z es 1/(b-a) sobre [a, b], y cero en cualquier otro lugar. Puedes calcular E (Z) usando el siguiente procedimiento:

Si a=1 y b=5, la media de Z ~ Uniform(1, 5) es simplemente (1+5)/2 = 3. Eso coincide con nuestra intuición. Si cada uno de los infinitos valores entre 1 y 5 tiene la misma probabilidad, esperaríamos que la media funcionara como el promedio simple de 1 y 5.

Ahora, odio desanimarte, pero en la práctica, es más probable que veas arcoíris dobles aterrizando en tu jardín delantero que encontrarte con variables aleatorias continuas para las que usarás el método integral para calcular su valor esperado.

Verás, las PDFs que parecen encantadoras y que se pueden integrar para obtener el valor esperado de las variables correspondientes tienen la costumbre de enclaustrarse en los ejercicios de fin de capítulo de los libros universitarios. Son como gatos domésticos. No salen afuera. Pero como estadístico en ejercicio, “afuera” es donde vives. Ahí fuera, te encontrarás mirando muestras de datos de valores continuos como las longitudes de los vehículos. Para modelar la PDF de tales variables aleatorias del mundo real, es probable que uses una de las funciones continuas conocidas como la Normal, la Log-Normal, la Chi-cuadrado, la Exponencial, la Weibull y así sucesivamente, o una distribución de mezcla, es decir, cualquier cosa que parezca adaptarse mejor a tus datos.

Aquí hay un par de tales distribuciones:

Para muchas PDFs comúnmente utilizadas, alguien ya ha tomado la molestia de derivar la media de la distribución mediante la integración ( x veces f(x) ) tal como lo hicimos con la distribución Uniforme. Aquí hay un par de tales distribuciones:

Finalmente, en algunas situaciones, en realidad en muchas situaciones, los conjuntos de datos de la vida real presentan patrones demasiado complejos para ser modelados por cualquiera de estas distribuciones. Es como cuando te contagias con un virus que te ataca con un montón de síntomas. Para ayudarte a superarlos, tu médico te receta un cóctel de medicamentos, cada uno con una fuerza, dosis y mecanismo de acción diferentes. Cuando te bombardean con datos que presentan muchos patrones complejos, debes desplegar un pequeño ejército de distribuciones de probabilidad para modelarlos. Tal combinación de diferentes distribuciones se conoce como una distribución mixta. Una mezcla común es la poderosa Mixtura Gaussiana, que es una suma ponderada de varias funciones de densidad de probabilidad de varias variables aleatorias normalmente distribuidas, cada una con una combinación diferente de media y varianza.

Dado un conjunto de datos de valores reales, es posible que te encuentres haciendo algo terriblemente simple: tomarás el promedio de la columna de datos de valores continuos y lo ungirás como la media muestral. Por ejemplo, si calculas la longitud promedio de los automóviles en el conjunto de datos de automóviles, obtendrás 174,04927 pulgadas, y ya está. Todo hecho. Pero eso no es todo y todo no está hecho. Porque todavía hay una pregunta que debes responder.

¿Qué tan buena es tu media muestral? Obtener una idea de su precisión

¿Cómo sabes qué tan precisa es tu media muestral como estimación de la media poblacional? Al recopilar los datos, puedes haber tenido mala suerte, o haber sido perezoso, o “limitado por los datos” (que a menudo es un excelente eufemismo para la buena y vieja pereza). De cualquier manera, estás mirando una muestra que no es proporcionalmente aleatoria. No representa proporcionalmente las diferentes características de la población. Tomemos el ejemplo del conjunto de datos de automóviles: es posible que hayas recopilado datos para un gran número de autos del tamaño de Zepes, y para muy pocos autos grandes. Y los limusines pueden estar completamente ausentes de tu muestra. Como resultado, la longitud media que calculas estará excesivamente sesgada hacia la longitud media solo de los autos del tamaño de Zepes en la población. Te guste o no, ahora estás trabajando en la creencia de que prácticamente todo el mundo conduce un automóvil del tamaño de Zepes.

Sé fiel a ti mismo

Si has recopilado una muestra muy sesgada y no lo sabes o no te importa, que el cielo te ayude en tu carrera elegida. Pero si estás dispuesto a considerar la posibilidad de sesgo y tienes algunas pistas sobre qué tipo de datos puedes estar perdiendo (por ejemplo, autos deportivos), entonces la estadística vendrá en tu ayuda con poderosos mecanismos para ayudarte a estimar este sesgo.

Desafortunadamente, no importa cuánto intentes, nunca podrás reunir una muestra perfectamente equilibrada. Siempre contendrá sesgos porque las proporciones exactas de varios elementos dentro de la población permanecen para siempre inaccesibles para ti. ¿Recuerdas esa puerta a la población? ¿Recuerdas cómo el letrero siempre dice “CERRADO”?

Tu curso de acción más efectivo es reunir una muestra que contenga aproximadamente las mismas fracciones de todas las cosas que existen en la población, la llamada muestra bien equilibrada. La media de esta muestra bien equilibrada es la mejor media muestral posible con la que puedes navegar.

Pero las leyes de la naturaleza no siempre cortan las velas de los barcos de estadísticos. Hay una magnífica propiedad de la naturaleza expresada en un teorema llamado el Teorema del Límite Central (TLC). Puedes usar el TLC para determinar qué tan bien tu media muestral estima la media poblacional.

El TLC no es una bala de plata para tratar con muestras gravemente sesgadas. Si tu muestra consiste predominantemente en automóviles de tamaño mediano, has redefinido efectivamente tu noción de la población. Si estás estudiando intencionalmente solo automóviles de tamaño mediano, estás absuelto. En esta situación, siéntete libre de usar el TLC. Te ayudará a estimar qué tan cerca está tu media muestral de la media poblacional de automóviles de tamaño mediano.

Por otro lado, si tu propósito existencial es estudiar toda la población de vehículos producidos, pero tu muestra contiene principalmente automóviles de tamaño mediano, tienes un problema. Para el estudiante de estadística, permíteme reformularlo en palabras ligeramente diferentes. Si tu tesis universitaria trata sobre con qué frecuencia bostezan las mascotas, pero tus reclutas son 20 gatos y el Caniche de tu vecino, entonces, con TLC o sin TLC, ninguna cantidad de habilidades estadísticas te ayudará a evaluar la precisión de tu media muestral.

La esencia del TCL

Una comprensión completa del TCL es tema para otro artículo, pero la esencia de lo que dice es lo siguiente:

Si se extrae una muestra aleatoria de puntos de datos de la población y se calcula la media de la muestra, y luego se repite este ejercicio muchas veces, se obtendrán… muchas medias de muestra diferentes. ¡Bueno, obvio! Pero algo asombroso sucede después. Si se traza una distribución de frecuencia de todas estas medias de muestra, se verá que siempre están distribuidas normalmente. Además, la media de esta distribución normal es siempre la media de la población que se está estudiando. Es esta faceta inquietantemente cautivadora de la personalidad de nuestro universo la que el Teorema del Límite Central describe utilizando (¿qué más?) el lenguaje de las matemáticas.

Veamos cómo utilizar el TCL. Comencemos así:

Usando la media de la muestra Z _bar de solo una muestra, diremos que la probabilidad de que la media de la población μ se encuentre en el intervalo [μ_bajo, μ_alto] es (1 — α):

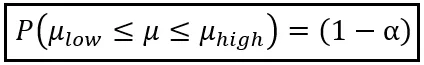
Se puede establecer α en cualquier valor de 0 a 1. Por ejemplo, si se establece α en 0,05, se obtendrá (1 — α) como 0,95, es decir, 95%.

Y para que esta probabilidad (1 — α) sea verdadera, los límites μ_bajo y μ_alto deben calcularse de la siguiente manera:

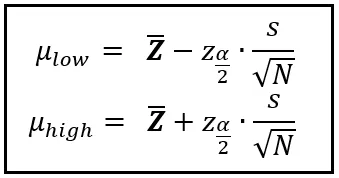
En las ecuaciones anteriores, sabemos cuáles son Z _bar, α, μ_bajo y μ_alto. El resto de los símbolos merecen alguna explicación.

La variable s es la desviación estándar de la muestra de datos.

N es el tamaño de la muestra.

Ahora llegamos a z_α/2.

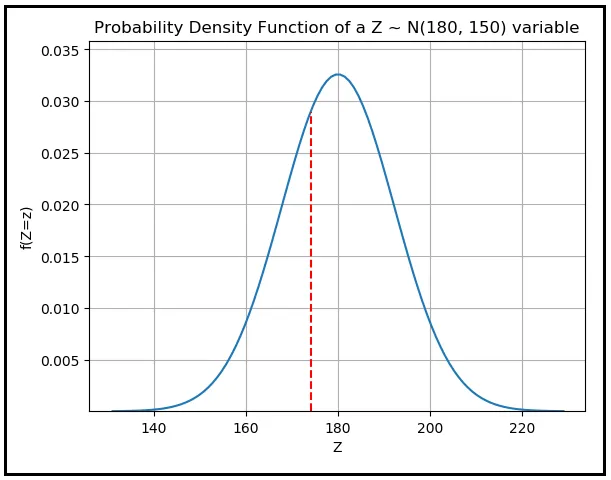
z_α/2 es un valor que se leerá en el eje X del PDF de la distribución normal estándar. La distribución normal estándar es el PDF de una variable aleatoria continua distribuida normalmente que tiene una media cero y una desviación estándar de uno. z_α/2 es el valor en el eje X de esa distribución para el cual el área debajo del PDF que se encuentra a la izquierda de ese valor es (1 — α/2). Así es cómo se ve esta área cuando se establece α en 0,05:

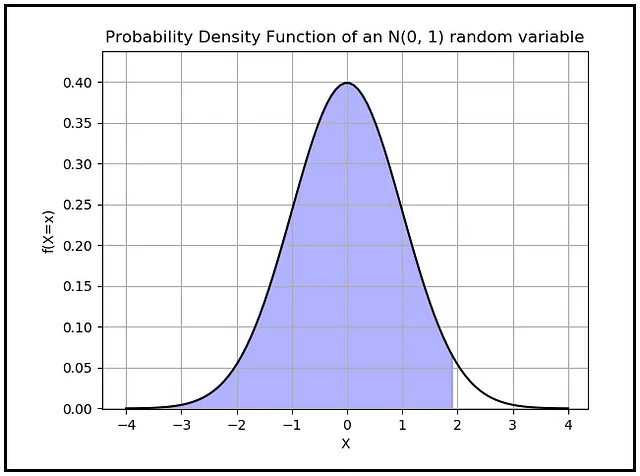
El área de color azul se calcula como (1 — 0,05/2) = 0,975. Recordemos que el área total debajo de cualquier curva PDF siempre es 1,0.

Para resumir, una vez que se ha calculado la media (Z _bar) de solo una muestra, se pueden construir límites alrededor de esta media de tal manera que la probabilidad de que la media de la población se encuentre dentro de esos límites sea un valor de su elección.

Reexaminemos las fórmulas para estimar estos límites:

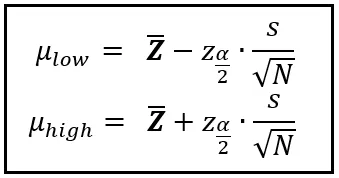
Estas fórmulas nos brindan algunas ideas sobre la naturaleza de la media de la muestra:

1. A medida que la varianza s de la muestra aumenta, el valor del límite inferior (μ_bajo) disminuye, mientras que el del límite superior (μ_alto) aumenta. Esto mueve efectivamente a μ_bajo y μ_alto aún más alejados uno del otro y lejos de la media de la muestra. Por el contrario, a medida que la varianza de la muestra disminuye, μ_bajo se acerca a Z _bar desde abajo, y μ_alto se acerca a Z _bar desde arriba. Los límites del intervalo convergen esencialmente en la media de la muestra desde ambos lados. En efecto, el intervalo [μ_bajo, μ_alto] es directamente proporcional a la varianza de la muestra. Si la muestra está ampliamente (o estrechamente) dispersa alrededor de su media, la mayor (o menor) dispersión reduce (o aumenta) la confiabilidad de la media de la muestra como una estimación de la media de la población.
2. Observe que el ancho del intervalo es inversamente proporcional al tamaño de la muestra (N). Entre dos muestras que exhiben varianza similar, la muestra más grande proporcionará un intervalo más estrecho alrededor de su media que la muestra más pequeña.

Veamos cómo calcular este intervalo para el conjunto de datos de automóviles. Calcularemos [μ_bajo, μ_alto] de tal manera que haya un 95% de probabilidad de que la media de la población μ se encuentre dentro de estos límites.

Para obtener una probabilidad del 95%, debemos configurar α en 0,05 para que (1 — α) = 0,95.

Sabemos que Z _bar es 174,04927 pulgadas.

N es de 205 vehículos.

La desviación estándar de la muestra se puede calcular fácilmente. Es de 12,33729 pulgadas.

A continuación, trabajaremos en z_α/2. Como α es 0,05, α/2 es 0,025. Queremos encontrar el valor de z_α/2 es decir z_0.025. Este es el valor en el eje X de la curva PDF de la variable aleatoria normal estándar, donde el área bajo la curva es (1 — α/2) = (1 — 0,025) = 0,975. Al referirnos a la tabla de la distribución normal estándar, encontramos que este valor corresponde al área a la izquierda de X =1,96.

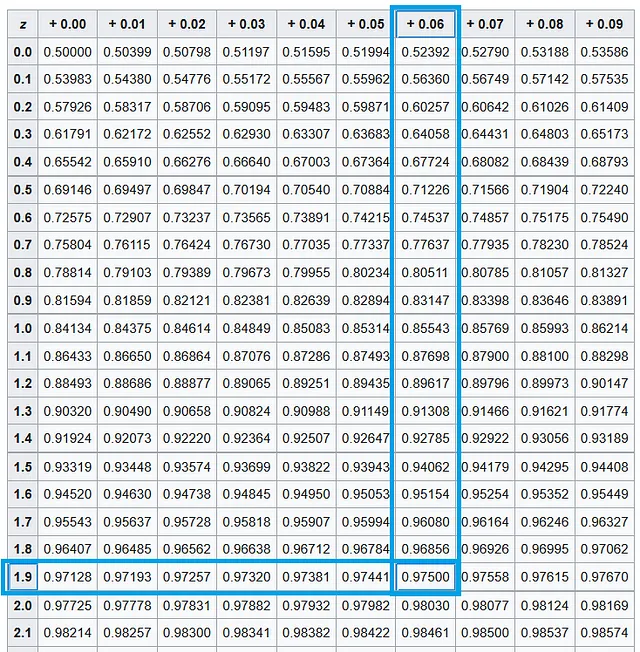
Sustituyendo todos estos valores, obtenemos los siguientes límites:

μ_bajo = Z_bar — ( z_α/2 · s/√N) = 174,04927 — (1,96 · 12,33729/205) = 173,93131

μ_alto = Z_bar + ( z_α/2 · s/√N) = 174,04927 + (1,96 · 12,33729/205) = 174,16723

Por lo tanto, [μ_bajo, μ_alto] = [173,93131 pulgadas, 174,16723 pulgadas]

Hay un 95% de probabilidad de que la media de la población se encuentre en este intervalo. Observa lo ajustado que es este intervalo. Su ancho es de solo 0,23592 pulgadas. Dentro de esta pequeña abertura se encuentra la media de la muestra de 174,04927 pulgadas. A pesar de todos los sesgos que puedan estar presentes en la muestra, nuestro análisis sugiere que la media de la muestra de 174,04927 pulgadas es una estimación notablemente buena de la media desconocida de la población.

Más allá de la primera dimensión: Expectativa en un espacio de muestra multidimensional

Hasta ahora, nuestra discusión sobre la expectativa ha sido confinada a una sola dimensión, pero no tiene por qué ser así. Podemos extender fácilmente el concepto de expectativa a dos, tres o más dimensiones. Para calcular la expectativa sobre un espacio multidimensional, todo lo que necesitamos es una Función de Masa de Probabilidad (o Densidad) Conjunta que esté definida sobre el espacio N-dim. Una PMF o PDF conjunta toma múltiples variables aleatorias como parámetros y devuelve la probabilidad de observar simultáneamente esos valores.

Anteriormente en el artículo, definimos una variable aleatoria Y que representa el número de cilindros en un vehículo elegido al azar del conjunto de datos de autos. Y es su quintessential única variable aleatoria discreta dimensional y su valor esperado se da por la siguiente ecuación:

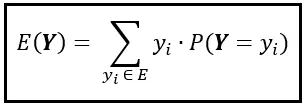
Presentemos una nueva variable aleatoria discreta, X. La Función de Masa de Probabilidad Conjunta de X e Y se denota por P( X =x_i, Y =y_j), o simplemente por P( X , Y ). Esta PMF conjunta nos saca del acogedor espacio unidimensional que Y habita y nos deposita en un espacio bidimensional más interesante. En este espacio 2D, un solo punto de datos o resultado se representa por la tupla (x_i, y_i). Si el rango de X contiene ‘p’ resultados y el rango de Y contiene ‘q’ resultados, el espacio 2D tendrá (p x q) resultados conjuntos. Usamos la tupla (x_i, y_i) para denotar cada uno de estos resultados conjuntos. Para calcular E( Y ) en este espacio 2D, debemos adaptar la fórmula de E( Y ) de la siguiente manera:

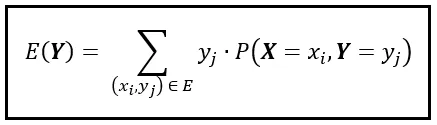
Observe que estamos sumando sobre todas las posibles tuplas (x_i, y_i) en el espacio 2D. Descompongamos esta suma en una suma anidada de la siguiente manera:

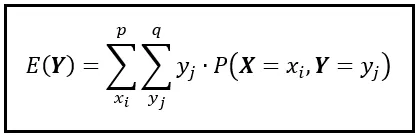
En la suma anidada, la suma interior calcula el producto de y_j y P( X =x_i, Y =y_j) sobre todos los valores de y_j. Luego, la suma exterior repite la suma interior para cada valor de x_i. Después, recopila todas estas sumas individuales y las suma para calcular E( Y ).

Podemos extender la fórmula anterior a cualquier número de dimensiones simplemente anidando las sumas dentro de cada una. Todo lo que necesita es una PMF conjunta que esté definida sobre el espacio N-dimensional. Por ejemplo, así es como se extiende la fórmula al espacio 4D:

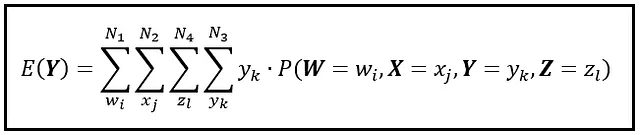
Observe cómo siempre estamos posicionando la suma de Y en el nivel más profundo. Puede organizar las sumas restantes en cualquier orden que desee: obtendrá el mismo resultado para E( Y ).

Puede preguntarse, ¿por qué querría definir una función de masa de probabilidad conjunta y volverse loco trabajando a través de todas esas sumas anidadas? ¿Qué significa E( Y ) cuando se calcula en un espacio N-dimensional?

La mejor manera de entender el significado de la esperanza en un espacio multidimensional es ilustrar su uso en datos multidimensionales del mundo real.

Los datos que usaremos provienen de un cierto barco que, a diferencia del que tomé para cruzar el Canal de la Mancha, no llegó al otro lado trágicamente.

La siguiente figura muestra algunas de las filas en un conjunto de datos de 887 pasajeros a bordo del RMS Titanic:

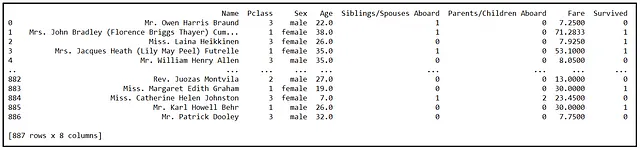
La columna Pclass representa la clase de cabina del pasajero con valores enteros de 1, 2 o 3. Las variables Siblings/Spouses Aboard y Parents/Children Aboard son variables binarias (0/1) que indican si el pasajero tenía hermanos, cónyuges, padres o hijos a bordo. En estadística, comúnmente, y algo cruelmente, nos referimos a tales variables indicadoras binarias como variables indicadoras ficticias. No hay nada obtuso en ellas que merezca el apodo despectivo.

Como puede ver en la tabla, hay 8 variables que identifican conjuntamente a cada pasajero en el conjunto de datos. Cada una de estas 8 variables es una variable aleatoria. La tarea que tenemos por delante es triple:

1. Queremos definir una función de masa de probabilidad conjunta sobre un subconjunto de estas variables aleatorias, y,
2. Usando esta función de masa de probabilidad conjunta, queremos ilustrar cómo calcular el valor esperado de una de estas variables sobre esta función de masa de probabilidad multidimensional, y,
3. Queremos entender cómo interpretar este valor esperado.

Para simplificar las cosas, “agruparemos” la variable Age en grupos de tamaño 5 años y etiquetaremos los grupos como 5, 10, 15, 20,…,80. Por ejemplo, una edad agrupada de 20 significará que la edad real del pasajero se encuentra en el intervalo de (15, 20] años. Llamaremos a la variable aleatoria agrupada como Age_Range.

Una vez que Age esté agrupado, agruparemos los datos por Pclass y Age_Range. Aquí están las cuentas agrupadas:

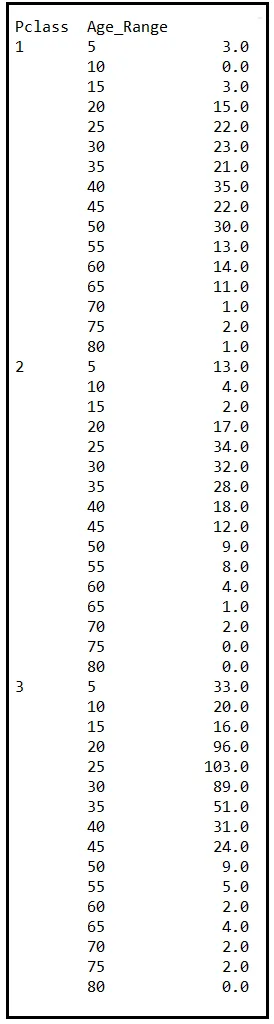
La tabla anterior contiene la cantidad de pasajeros a bordo del Titanic para cada cohorte (grupo) que está definido por las características Pclass y Age_Range. Por cierto, cohorte es otra palabra (junto con asintótico) que los estadísticos adoran. Aquí hay un consejo: cada vez que quieras decir “grupo”, solo di “cohorte”. Te prometo que esto, lo que sea que estuvieras planeando decir, sonará instantáneamente diez veces más significativo. Para ilustrar: “Se les dio vino falso a ocho cohortes diferentes de entusiastas del alcohol (perdóneme, oenófilos) para beber y se registraron sus reacciones”. ¿Ves a lo que me refiero?

Para ser honesto, “cohorte” lleva un significado preciso que “grupo” no tiene. Aún así, puede ser instructivo decir “cohorte” de vez en cuando y observar cómo crecen los sentimientos de respeto en las caras de sus oyentes.

En cualquier caso, agregaremos otra columna a la tabla de frecuencias. Esta nueva columna contendrá la probabilidad de observar la combinación particular de Pclass y Age_Range. Esta probabilidad, P(Pclass, Age_Range), es la razón de la frecuencia (es decir, el número en la columna Name) al número total de pasajeros en el conjunto de datos (es decir, 887).

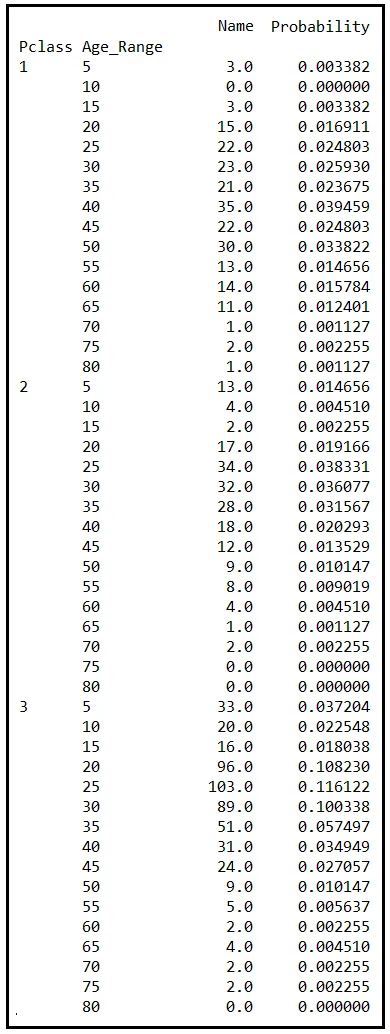
La probabilidad P(Pclass, Age_Range) es la Función de Masa de Probabilidad Conjunta de las variables aleatorias Pclass y Age_Range. Nos da la probabilidad de observar un pasajero que está descrito por una combinación particular de Pclass y Age_Range. Por ejemplo, observe la fila donde Pclass es 3 y Age_Range es 25. La correspondiente probabilidad conjunta es 0.116122. Ese número nos dice que aproximadamente el 12% de los pasajeros en las cabinas de tercera clase del Titanic tenían entre 20 y 25 años.

Al igual que con la PMF unidimensional, la PMF conjunta también se suma a 1.0 cuando se evalúa sobre todas las combinaciones de valores de sus variables aleatorias constituyentes. Si su PMF conjunta no se suma a 1.0, debe examinar detenidamente cómo la ha definido. Puede haber un error en su fórmula o, peor aún, en el diseño de su experimento.

En el conjunto de datos anterior, la PMF conjunta suma efectivamente a 1.0. ¡Siéntase libre de creerme!

Para tener una idea visual de cómo se ve la PMF conjunta, P(Pclass, Age_Range), puede trazarla en 3 dimensiones. En el gráfico 3D, establezca el eje X e Y respectivamente en Pclass y Age_Range y el eje Z en la probabilidad P(Pclass, Age_Range). Lo que verá es un fascinante gráfico 3D.

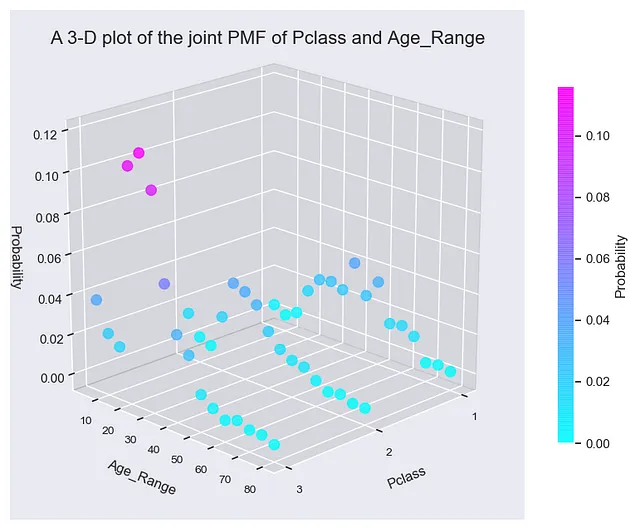
Si observa detenidamente el gráfico, notará que la PMF conjunta consiste en tres gráficos paralelos, uno para cada clase de cabina en el Titanic. El gráfico 3D muestra algunas de las estadísticas demográficas de la humanidad a bordo del desafortunado transatlántico. Por ejemplo, en las tres clases de cabina, los pasajeros de entre 15 y 40 años fueron los que conformaron la mayor parte de la población.

Ahora trabajemos en el cálculo de E(Age_Range) sobre este espacio 2D. E(Age_Range) se da por:

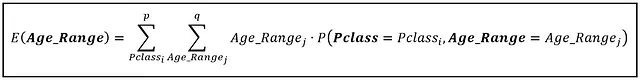
Ejecutamos la suma interna sobre todos los valores de Age_Range: 5,10,15,…,80. Ejecutamos la suma externa sobre todos los valores de Pclass: [1, 2, 3]. Para cada combinación de (Pclass, Age_Range), seleccionamos la probabilidad conjunta de la tabla. El valor esperado de Age_Range es de 31.48252537 años, lo que corresponde al valor binado de 35. Podemos esperar que el pasajero ‘promedio’ en el Titanic tenga entre 30 y 35 años.

Si tomas la media de la columna de Age_Range en el conjunto de datos del Titanic, llegarás exactamente al mismo valor: 31.48252537 años. Entonces, ¿por qué no tomar simplemente el promedio de la columna de Age_Range para obtener E( Age_Range) ? ¿Por qué construir una máquina de Rube Goldberg de sumas anidadas sobre un espacio N-dimensional solo para llegar al mismo valor?

Es porque en algunas situaciones, todo lo que tendrás es la PMF conjunta y los rangos de las variables aleatorias. En este caso, si solo tuvieras P( Pclass, Age_Range ) y supieras que el rango de Pclass es [1,2,3], y que el de Age_Range es [5,10,15,20,…,80], aún puedes usar la técnica de sumas anidadas para calcular E( Pclass ) o E( Age_Range ).

Si las variables aleatorias son continuas, el valor esperado sobre un espacio multidimensional se puede encontrar utilizando una integral múltiple. Por ejemplo, si X , Y , y Z son variables aleatorias continuas y f( X , Y , Z ) es la función de densidad de probabilidad conjunta definida sobre el espacio continuo tridimensional de tuplas (x, y, z), el valor esperado de Y sobre este espacio tridimensional se muestra en la siguiente figura:

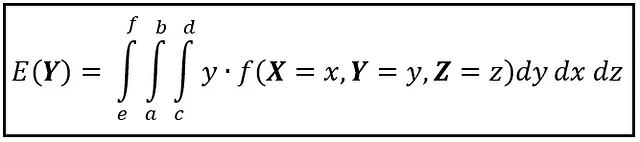
Al igual que en el caso discreto, primero se integra sobre la variable cuyo valor esperado se desea calcular, y luego se integra sobre el resto de las variables.

Existe un famoso ejemplo que demuestra la aplicación del método de integral múltiple para calcular valores esperados a una escala demasiado pequeña para que el ojo humano lo perciba. Me refiero a la función de onda de la mecánica cuántica. La función de onda se denota como Ψ(x, y, z, t) en coordenadas cartesianas o como Ψ(r, θ, ɸ, t) en coordenadas polares. Se utiliza para describir las propiedades de cosas seriamente diminutas que disfrutan viviendo en espacios realmente, realmente estrechos, como los electrones en un átomo. La función de onda Ψ devuelve un número complejo de la forma A + jB, donde A representa la parte real y B representa la parte imaginaria. Podemos interpretar el cuadrado del valor absoluto de Ψ como una función de densidad de probabilidad conjunta definida sobre el espacio de cuatro dimensiones descrito por la tupla (x, y, z, t) o (r, θ, ɸ, t). Específicamente para un electrón en un átomo de hidrógeno, podemos interpretar |Ψ|² como la probabilidad aproximada de encontrar al electrón en un volumen infinitesimalmente pequeño de espacio alrededor de (x, y, z) o alrededor de (r, θ, ɸ) en el tiempo t. Al conocer |Ψ|², podemos ejecutar una integral cuádruple sobre x, y, z, y t para calcular la ubicación esperada del electrón a lo largo del eje X, Y o Z (o sus equivalentes polares) en el tiempo t.

Pensamientos finales

Comencé este artículo con mi experiencia con el mareo. Y no te culparía si te retorcieras ante el uso descarado de una variable aleatoria de Bernoulli para modelar lo que es un trastorno humano notablemente complejo y algo mal entendido. Mi objetivo era ilustrar cómo la expectativa nos afecta, literalmente, a nivel biológico. Una forma de explicar ese trastorno fue usar el lenguaje fresco y reconfortante de las variables aleatorias.

Comenzando con la variable Bernoulli, aparentemente simple pero engañosa, pasamos nuestro pincel ilustrativo a través del lienzo estadístico hasta llegar a la magnífica complejidad multidimensional de la función de onda cuántica. En todo momento, buscamos comprender cómo la expectativa opera en escalas discretas y continuas, en una y múltiples dimensiones, y a escala microscópica.

Hay una área más en la que la expectativa tiene un impacto inmenso. Esa área es la probabilidad condicional en la que se calcula la probabilidad de que una variable aleatoria X tome un valor ‘x’ asumiendo que ciertas otras variables aleatorias A, B, C, etc. ya han tomado valores ‘a’, ‘b’, ‘c’. La probabilidad de X condicionada a A, B y C se denota como P( X =x| A =a, B =b, C =c) o simplemente como P( X | A , B , C ). En todas las fórmulas de expectativa que hemos visto, si reemplaza la probabilidad (o densidad de probabilidad) con la versión condicional de la misma, lo que obtendrá son las fórmulas correspondientes para la expectativa condicional. Se denota como E( X =x| A =a, B =b, C =c) y se encuentra en el corazón de los extensos campos del análisis de regresión y la estimación. ¡Y eso es alimento para futuros artículos!

Citaciones y Derechos de Autor

Conjunto de Datos

El conjunto de datos de automóviles se descarga del Repositorio de Aprendizaje Automático de UC Irvine bajo la licencia Creative Commons Attribution 4.0 International (CC BY 4.0).

El conjunto de datos de Titanic se descarga de Kaggle bajo la licencia CC0.

Imágenes

Todas las imágenes de este artículo son propiedad de Sachin Date bajo CC-BY-NC-SA, a menos que se mencione una fuente y derechos de autor diferentes debajo de la imagen.

Si le gustó este artículo, sígame en Sachin Date para recibir consejos, tutoriales y consejos de programación sobre temas dedicados a la regresión, el análisis de series de tiempo y la previsión.

We will continue to update Zepes; if you have any questions or suggestions, please contact us!